মহাকর্ষ ও অভিকর্ষ
এই অধ্যায়ের সকল টপিকস সমূহ
মহাকর্ষের ভিত্তি রচনা করেছিলেন স্যার আইজ্যাক নিউটন । তার এই তত্ত্বের কিছুটা সীমাবদ্ধতাও ছিল । যা উল্লেখ করে এই শাখাটির উন্নতি সাধন করেন বিজ্ঞানী কেপলার । এই অধ্যায়ে মূলত এই দুইটি বিষয় নিয়েই বিষদ আলোচনা করা হয়েছে । তাই আমরা প্রথমে নিউটন এবং কেপলারের সূত্রের বিষদ আলোচনা করব এবং পরবর্তীতে বাস্তব জীবনে এর কিছু প্রয়োগ আলোচনা করব ।
টপিকস - 6.1: কেপলারের সূত্র ।
কেপলারের সূত্র
নিউটনের এই সমীকরণের লেখচিত্র ছিল উপবৃত্তের । কিন্তু তিনি সূর্যকে কেন্দ্র করে পৃথিবীর ঘূর্ণনের কক্ষপথ বৃত্তাকার বলে উল্লেখ করেন । যদিও তার সূত্র উপবৃত্তের যৌক্তিকতা দেয় । তার এই সীমাবদ্ধতাকে উল্লেখ করে বিজ্ঞানী কেপলার উপবৃত্তের ধারণা সহ আরও দুইটি সূত্র দেন । যা নিম্নরুপঃ
১। উপবৃত্তের সূত্রঃ
কেপলারের উপবৃত্তের সূত্রটি হল- পৃথিবী সূর্যের চারদিকে বৃত্তাকার নয় বরং উপবৃত্তাকার কক্ষপথে ঘুরছে ।
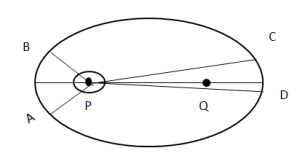
যদি বৃত্তাকার পথের কথা বলা হত, আমরা নির্দ্বিধায় বলে দিতে পারতাম, সূর্য এই বৃত্তাকার কক্ষপথের কেন্দ্রে আছে । কিন্তু যেহেতু উপবৃত্তাকার কক্ষপথের কথা বলা হয়েছে তাই প্রশ্ন থেকে যায়, সূর্য এই উপবৃত্তের কোথায় আছে ? এমন প্রশ্নের জবাবে কেপলার উল্লেখ করেন, সূর্য এই উপবৃত্তাকার কক্ষপথের যেকোনো একটি ফোকাসে (P অথবা Q) আছে । কেন্দ্রে নয় । তাহলে সামষ্টিক ভাবে তার উপবৃত্তের সূত্রটি দাঁড়ালো, “পৃথিবী সূর্যকে তার ফোকাসে রেখে একটি নির্দিষ্ট উপবৃত্তাকার কক্ষপথে পরিভ্রমণ করছে ।”
উপবৃত্তাকার কক্ষপথের সূত্রের পরই প্রশ্ন থেকে যায়, তাহলে এই উপবৃত্তাকার কক্ষপথে গ্রহটির বেগ কেমন হবে ? এই প্রশ্নের জবাব দেয় তার দ্বিতীয় সূত্র ।
২। ক্ষেত্রফলের সূত্রঃ
মনে কর, যেকোনো মুহূর্তে গ্রহটি A বিন্দুতে আছে এবং 5 দিনে এটি B বিন্দুতে চলে গেল । আবার যেকোনো মুহূর্তে এটি C বিন্দুতে ছিল এবং 5 দিনে এটি D বিন্দুতে চলে গেল । গ্রহটির বেগ এমন হবে যেন, এই দুই ক্ষেত্রফল সমান হয় কারণ এক্ষেত্রে সময় সমান ছিল । বুঝতেই পারছো, এমনটা হতে গেলে গ্রহটি যখন সূর্যের কাছাকাছি থাকবে তখন এই বেগ বেশি হবে এবং দূরে থাকবে, তখন এর বেগ কম হবে ।
তাহলে সূত্রটি দাঁড়ালো- “গ্রহ ও সূর্যের সংযোগকারী ব্যাসার্ধরেখা সমান সময়ে সমান ক্ষেত্রফল উৎপন্ন করবে ।”
এবার প্রশ্ন থেকে যায়, তাহলে গ্রহটির পর্যায়কাল কেমন হবে ? অর্থাৎ কত দিনে এক বছর হবে । এ প্রশ্নের জবাব পাওয়া যায় কেপলারের তৃতীয় সূত্র থেকে । যা পর্যায়কালের সূত্র নামে পরিচিত ।
৩। পর্যায়কালের সূত্রঃ
চিত্রে P ও Q বিন্দুগামী উপবৃত্তের দুই পরিধি বরাবর যে রেখা দেখতে পারছি, তাকে বলা হয় উপবৃত্তের পরাক্ষ । যার দৈর্ঘ্যকে 2a দ্বারা প্রকাশ করা হয় । এখন যদি গ্রহটির পর্যায়কাল T হয় তবে এদের মধ্যে সম্পর্ক হবে,
\(T^2\propto\left(2a\right)^3\)
অর্থাৎ, “গ্রহটির পর্যায়কালের বর্গ পরাক্ষের ঘন এর সমানুপাতিক।”
আমরা একে লিখতে পারি,
\(T^2=k.\left(2a\right)^3=k.8.a^3\)
\(T^2\propto a^3\) [যেহেতু k ধ্রুবক, তাই 8k ধ্রুবক হবে]
সুতরাং আমরা বলতে পারি, “পর্যায়কালের বর্গ অর্ধপরাক্ষের ঘন এর সমানুপাতিক ।”
আপাতভাবে আমরা যদি সূর্যের চারদিকে পৃথিবীর কক্ষপথকে R ব্যাসার্ধের বৃত্তাকার চিন্তা করি তাহলে লেখা যায়,
\(T^2\propto R^3\)
\(T^2=k.R^3\)
\(\frac{T_1^2}{R_1^3}=\frac{T_2^2}{R_2^3}\)
এ সম্পর্ক থেকে আমরা নিশ্চয়ই বুঝতে পারছি, সূর্য থেকে গ্রহটি যত দূরে অবস্থান করবে এর পর্যায়কাল তত বেশি হবে । অর্থাৎ এক বছরে এর দিনের সংখ্যা আরও বেশি হবে।
আসছে…
আসছে…
টপিকস - 6.2: নিউটনের সূত্র ।
নিউটনের সূত্র
কুলম্বের সূত্রের অনুরূপ আমরা নিউটনের সূত্রে পড়েছিলাম, মহাবিশ্বের প্রত্যেকটি বস্তুকণা একে অপরকে আকর্ষণ করে । এই আকর্ষণ বা বিকর্ষণ বলের মান, এদের ভরের গুণফলের সমানুপাতিক এবং মধ্যবর্তী দূরত্বের বর্গের ব্যাস্তানুপাতিক । এই বল এদের সংযোজক সরলরেখা বরাবর ক্রিয়া করে ।
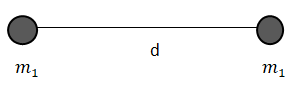
মনে কর, \(m_1\) এবং \(m_2\) ভরের দুইটি বস্তু পরস্পর হতে d দূরত্বে অবস্থান করছে ।
এখন নিউটনের সূত্রানুসারে,
\(F\propto m_1\times m_2\)
\(F\propto\frac1{d^2}\)
একত্রে লেখা যায়, \(F\propto\frac{m_1\times m_2}{d^2}\)
সুতরাং, \(F=\frac{Gm_1m_2}{d^2}\) [এখানে, G মহাকর্ষীয় সার্বজনীন ধ্রুবক বা বিশ্বজনীন ধ্রুবক]
এখন, \(G=\frac{F.d^2}{m_1.m_2}\)
সুতরাং G এর, একক \(=\frac{N.m^2}{kg^2}=Nm^2kg^{-2}\)
মাত্রা \(=\frac{MLT^{-2}.L^2}{M^2}=\left[M^{-1}L^3T^{-2}\right]\)
সংজ্ঞাঃ \(G=\frac{F.d^2}{m_1.m_2}\) সমীকরণে, \(m_1=1\), \(m_2=1\), \(d=1\) হলে, G=F অর্থাৎ যা F তাই G ।
সুতরাং, একক ভরের দুইটি বস্তু পরস্পর হতে একক দূরত্বে অবস্থান করলে পরস্পরকে যে মহাকর্ষীয় বলে আকর্ষণ করে তাকে বলা মহাকর্ষীয় সার্বজনীন ধ্রুবক ।
আসছে…
আসছে…
টপিকস - 6.3: অভিকর্ষ এবং অভিকর্ষজ ত্বরণ ।
ধরে নিচ্ছি, পৃথিবী একটি গোলক সদৃশ এবং এর সমগ্র ভর এর কেন্দ্রে কেন্দ্রীভূত থাকে । এই ভর, M এবং পৃথিবীর ব্যাসার্ধ, R । একটি m ভরের বস্তু পৃথিবী পৃষ্ঠে রাখা হল । এখন বস্তু ও পৃথিবীর মধ্যকার আকর্ষণ বল বা যাকে আমরা অভিকর্ষ বল বলছি তা হবে,
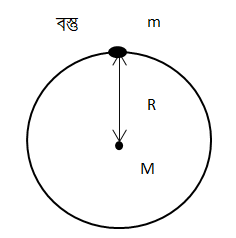
\(F=\frac{GMm}{R^2}\)
বা, \(mg=\frac{GMm}{R^2}\)
বা, \(g=\frac{GM}{R^2}\)
সুতরাং, \(g=\frac{GM}{R^2}\)
এখন, পৃথিবীর গড় ঘনত্ব ρ এবং আয়তন V হলে,
আমরা জানি, \(\rho=\frac MV\)
বা, \(M=\rho V=\rho\times\frac43\pi R^3\)
M এর মান (1) নং সমীকরণে বসাই,
\(g=\frac G{R^2}\times\rho\times\frac43\pi R^3=\frac43\pi R\rho G\)
সুতরাং, \(g=\frac{GM}{R^2}=\frac43\pi R\rho G\)
তাহলে আমরা অভিকর্ষজ ত্বরণ g নির্ণয়ের দুইটি সূত্র পেলাম । পৃথিবী পৃষ্ঠে অভিকর্ষজ ত্বরণ নির্ণয় করতে পারব । কোন গাণিতিক সমস্যায় যদি পৃথিবীর ভর দেয়া থাকে তাহলে প্রথম সূত্রটি এবং গড় ঘনত্ব দেয়া থাকলে দ্বিতীয় সূত্রটি প্রয়োগ করে সমাধান করা যাবে । তবে পৃথিবী ছাড়াও যেকোনো গ্রহের ভর বা ঘনত্ব দেয়া থাকলে সূত্রটি প্রয়োগ করে সেই গ্রহের অভিকর্ষজ ত্বরণ নির্ণয় করা যাবে ।
N.B: লক্ষ্য কর, অভিকর্ষজ ত্বরণের সূত্রে এমন কোন রাশি নেই যা বস্তুর উপর নির্ভর করে । নির্ভর করে শুধু পৃথিবীর ব্যাসার্ধ, ভর এবং ঘনত্বের উপর । তাই আমরা বলতে পারি, যেকোনো ভরের বস্তুর জন্য অভিকর্ষজ ত্বরণ একই হবে ।
আসছে…
আসছে…
টপিকস - 6.4: অভিকর্ষজ ত্বরণের নির্ভরশীলতা ।
অভিকর্ষজ ত্বরণের নির্ভরশীলতা
অভিকর্ষজ ত্বরণ বস্তুর উপর ভর বা উপাদানের উপর নির্ভর না করলেও এটি তিনটি বিষয়ের উপর নির্ভর করে । এগুলো হলঃ-
- পৃথিবীর আকৃতি ।
- বস্তুর ভৌগোলিক অবস্থান ।
- বস্তুর অক্ষীয় অবস্থান ।
১। পৃথিবীর আকৃতি
আমরা জানি,
\(g=\frac{GM}{R^2}\)
সূত্রটি দেখেই তোমরা নিশ্চয়ই বুঝতে পাড়ছ, যদি পৃথিবীর কেন্দ্র বা ভরকেন্দ্র থেকে বস্তুর দূরত্ব (R) বাড়ে তবে অভিকর্ষজ ত্বরণ কমবে এবং যদি দূরত্ব কমে তবে অভিকর্ষজ ত্বরণ বাড়বে ।
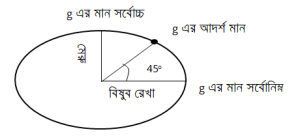
আমরা জানি, বিষুব অঞ্চলে R এর মান সর্বোচ্চ তাই g এর মান সর্বনিম্ন । মেরু অঞ্চলে R এর মান সর্বনিম্ন তাই g এর মান সর্বোচ্চ ।
তাই 45° অক্ষাংশে g এর মানকে আদর্শ মান ধরা হয় । কারণ, 45° অক্ষাংশে আমরা R এর মানকে গড়মান ধরতে পারি ।
N.B: পৃথিবী পৃষ্ঠস্থ কোন বস্তুর অবস্থান পৃথিবীর কেন্দ্রে এর অক্ষ রেখা বা বিষুব রেখার সাথে যে কোন উৎপন্ন করে তাকে তার অক্ষাংশ বলে ।
২। বস্তুর ভৌগোলিক অবস্থান
ধরে নিচ্ছি পৃথিবী বৃত্তাকার । ভৌগোলিক অবস্থানের দৃষ্টিকোণ থেকে বস্তু ভূপৃষ্ঠ হতে উপরে বা নিচে অবস্থান করতে পারে ।