ভেক্টর
এই অধ্যায়ের সকল টপিকস সমূহ
-
টপিকস - 2.1:
ভেক্টর এবং ভেক্টর রাশির প্রকাশ পদ্ধতি ।
-
টপিকস - 2.2:
ভেক্টর রাশির বিশেষত্ব, ত্রিমাত্রিক স্থানাংক ব্যবস্থায় ভেক্টর রাশির প্রকাশ এবং ভেক্টরের যোগ বিয়োগ।
-
টপিকস - 2.3:
বিশেষ ভেক্টর ।
-
টপিকস - 2.4:
ভেক্টর রাশির যোগের সূত্র, ত্রিমাত্রিক ভেক্টরের মান ও দিক, ত্রিমাত্রিক ভেক্টরের যোগ বিয়োগ ।
-
টপিকস - 2.5:
উপাংশের সূত্রের সাহায্যে বাস্তব ঘটনার ব্যাখ্যা ।
-
টপিকস - 2.6:
ভেক্টর যোগের সামান্তরিক সূত্রের ব্যবহার ।
-
টপিকস - 2.7:
নৌকা নদী সংক্রান্ত সমস্যা ।
-
টপিকস - 2.8:
বৃষ্টি ছাতা ধরা সংক্রান্ত সমস্যা ।
-
টপিকস - 2.9:
বৃষ্টিতে গাড়ির কাঁচ ভেজা সংক্রান্ত সমস্যা।
-
টপিকস - 2.10:
আপেক্ষিক বেগ সংক্রান্ত সমস্যা।
-
টপিকস - 2.11:
ভেক্টর রাশির গুণ ।
-
টপিকস - 2.12:
অপারেটর, গ্রেডিয়েন্ট, ডাইভারজেন্স, কার্ল অপারেটর ।
টপিকস - 2.1: ভেক্টর এবং ভেক্টর রাশির প্রকাশ পদ্ধতি ।
ভেক্টর কি
পদার্থবিজ্ঞানে এমন অনেক রাশি রয়েছে যেগুলো শুধুমাত্র মান দিয়ে সম্পূর্ণরূপে প্রকাশ করা যায় না । মানের সাথে দিকের ও প্রয়োজন হয় । সেই সকল রাশিকে বলা হয় ভেক্টর রাশি । মানের সাথে দিক জড়িত থাকায় এদের যোগ বা গুণ সাধারণ বীজগাণিতিক নিয়মে করা সম্ভব হয় না । যা কিছু বিশেষ নিয়মেই শুধুমাত্র করা যায় ।
ভেক্টর রাশির উদাহরণঃ বেগ, ত্বরণ, সরণ, টর্ক প্রভৃতি ।
আবার এমন অনেক রাশি রয়েছে যারা দিক ছাড়াই সম্পূর্ণতা প্রকাশ করতে পারে । যাদেরকে বলা হয় স্কেলার রাশি ।
স্কেলার রাশির উদাহরণঃ দ্রুতি, দৈর্ঘ্য, সময়, ভর, কাজ, চার্জ, কম্পাঙ্ক, বৈদ্যুতিক বিভব, স্বকীয় আবেশ গুণাঙ্ক, উষ্ণতা, তড়িৎ প্রবাহ প্রভৃতি ।
প্রকাশ পদ্ধতি
ভেক্টর রাশিকে চারভাবে প্রকাশ করা যেতে পারে । যথাঃ
১। A এর ভেক্টর রুপ \(=\overrightarrow A\) এবং মান \(=\left|\overrightarrow A\right|\)
২। A এর ভেক্টর রুপ \(=\overline A\) এবং মান \(=\left|\overline A\right|\)
৩। A এর ভেক্টর রুপ \(=\underline A\) এবং মান \(=\left|\underline A\right|\)
৪। A এর ভেক্টর রুপ \(=\boldsymbol A\) এবং মান \(=\left|\boldsymbol A\right|=A\)
ভেক্টর রাশি, মান এবং দিকের সম্পর্ক
সংজ্ঞাতেই আমরা পড়েছি, যে সকল রাশির মান এবং দিক আছে তাই ভেক্টর রাশি । সেই দৃষ্টিকোণ থেকে,
ভেক্টর রাশি = মান × দিক
বা, \(\overrightarrow A=\left|\overrightarrow A\right|\times\widehat a\)
\(\widehat a=\frac{\overrightarrow A}{\left|\overrightarrow A\right|}\)
অর্থাৎ, \(\overrightarrow A\) এর দিক বা \(\overrightarrow A\) বরাবর বা \(\overrightarrow A\) এর সমান্তরাল সকল ভেক্টরের একক ভেক্টর \(\widehat a=\frac{\overrightarrow A}{\left|\overrightarrow A\right|}\)
অর্থাৎ কোন ভেক্টরকে তার মান দ্বারা ভাগ করলে ঐ ভেক্টরের দিকে একটি একক ভেক্টর বা ভেক্টরটির দিক পাওয়া যায় ।
১। কোনটি স্কেলার রাশি ?
(ক) বল (খ) টর্ক (গ) তড়িৎ ফ্লাক্স (ঘ) তীব্রতা
২। কোনটি ভেক্টর রাশির প্রকাশ পদ্ধতি নয় ?
(ক) \(\overrightarrow A\) (খ) \(\overline{\overline A}\) (গ) \(\overrightarrow A\) (ঘ) A
১।গ ২।খ
টপিকস - 2.2: ভেক্টর রাশির বিশেষত্ব, ত্রিমাত্রিক স্থানাংক ব্যবস্থায় ভেক্টর রাশির প্রকাশ এবং ভেক্টরের যোগ বিয়োগ।
ভেক্টরের বিশেষত্ব
সাধারণ রাশি থেকে ভেক্টর রাশির বিশেষ কিছু ভিন্নতা বা বৈশিষ্ঠ রয়েছে । যেমন-
- ভেক্টর রাশির যোগ বা গুণ সাধারণ বীজগাণিতিক নিয়মে করা যায় না । কারণ এর মানের সাথে দিক জড়িত । তাই কিছু বিশেষ নিয়মে এর যোগ বা গুণ করতে হয় । যা পরবর্তীতে আলোচনা করা হয়েছে ।
- ভেক্টর তিনটি সূত্র মেনে চলে । যথাঃ
- বিনিময় সূত্র – \(\overrightarrow A+\overrightarrow B=\overrightarrow B+\overrightarrow A\)
- সংযোজন সূত্র – \(\left(\overrightarrow A+\overrightarrow B\right)+\overrightarrow C=\overrightarrow A+\left(\overrightarrow B+\overrightarrow C\right)\)
- বণ্ঠণ সূত্র – \(n\left(\overrightarrow A+\overrightarrow B\right)=n\overrightarrow A+n\overrightarrow B\)
উল্লেখ্য কোন একটি রাশিকে ভেক্টর রাশি হতে গেলে যেমন তার দিক থাকা জরুরী । তেমনি তার এই তিনটি সূত্রও মেনে নেয়া জরুরী ।
যেমনঃ তড়িৎ প্রবাহের দিক থাকা সত্ত্বেও এটি ভেক্টর যোগের বিনিময় সূত্র মেনে চলেনা বিধায় । তড়িৎ প্রবাহ স্কেলার রাশির অন্তর্ভুক্ত । তবে কিছু বিশেষ ক্ষেত্রে এর ভিন্নতা রয়েছে ।
মনে রেখোঃ ভেক্টর রাশির আর একটি বিশেষ বিশেষত্ব হল, এটিকে ইচ্ছে করলেই সমান্তরালে সরানো যায় । অর্থাৎ ভেক্টর রাশি অনুসারে, একটি সোজা ট্রেন লাইনের বাম পাশের লেন ধরে যাওয়া এবং ডান পাশের লেন ধরে যাওয়ার মধ্যে কোন পার্থক্য নেই ।
এই বিশেষত্বটি প্রয়োগ করে ভেক্টর রাশির অনেক সমস্যা সহজেই সমাধান করা সম্ভব ।
ত্রিমাত্রিক স্থানাংক ব্যবস্থায় ভেক্টর রাশির প্রকাশ
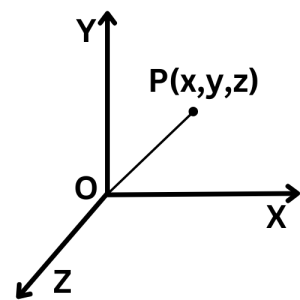
মনে কর, ত্রিমাত্রিক স্থানাঙ্কে কোন একটি বিন্দুর স্থানাঙ্ক P(x, y, z) । ত্রিমাত্রিক স্থানাঙ্ক ব্যবস্থায় X, Y এবং Z অক্ষ বরাবর যে তিনটি একক ভেক্টর যথাক্রমে \(\widehat i\), \(\widehat j\) এবং \(\widehat k\) বিবেচনা করা হয় ।
এখন,
মূলবিন্দু O হতে P বিন্দুতে গেলে সরণ
\(\overrightarrow{OP}=\) X অক্ষ বরাবর সরণ x + Y অক্ষ বরাবর সরণ y + Z অক্ষ বরাবর সরণ z
অর্থাৎ মূলবিন্দু O হতে P এর অবস্থান,
\(\overrightarrow{OP}=x\times\)X অক্ষের দিক + \(y\times\) Y অক্ষের দিক + \(z\times\) Z অক্ষের দিক
বা, \(\overrightarrow{OP}=x\times\)X অক্ষের দিকে একক ভেক্টর + \(y\times\) Y অক্ষের দিকে একক ভেক্টর + \(z\times\) Z অক্ষের দিকে একক ভেক্টর
\(\overrightarrow{OP}=x\widehat i+y\widehat j+z\widehat k=\overrightarrow P\)
সমকোণী ত্রিভুজে পিথাগোরাসের সূত্রানুসারে, \(\overrightarrow P\) ভেক্টরটির মান \(=\left|\overrightarrow P\right|=\sqrt{x^2+y^2+z^2}\)
আবার
মূলবিন্দু সাপেক্ষে কোন দুইটি বিন্দুর অবস্থান ভেক্টর যদি,
\(\overrightarrow{OP}=x_1\widehat i+y_1\widehat i+z_1\widehat i=\overrightarrow P\)
\(\overrightarrow{OQ}=x_2\widehat i+y_2\widehat i+z_2\widehat i=\overrightarrow Q\) হয়
তবে, \(\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}=\overrightarrow Q-\overrightarrow P=(x_2\widehat i+y_2\widehat i+z_2\widehat i)-(x_1\widehat i+y_1\widehat i+z_1\widehat i)\)
[অর্থাৎ শেষেরটি (Q) – আগেরটি (P) ]
ত্রিমাত্রিক ভেক্টরের যোগ ও বিয়োগ
মনে করি,
\(\overrightarrow A=A_x\widehat i+A_y\widehat j+A_z\widehat k\)
\(\overrightarrow B=B_x\widehat i+B_y\widehat j+B_z\widehat k\)
\(\overrightarrow R=\overrightarrow A+\overset{\;\rightarrow}B=\left(A_x+B_x\right)\widehat i+\left(A_y+B_y\right)\widehat j+\left(A_z+B_z\right)\widehat k\)
\(\overrightarrow S=\overrightarrow A-\overset{\;\rightarrow}B=\left(A_x-B_x\right)\widehat i+\left(A_y-B_y\right)\widehat j+\left(A_z-B_z\right)\widehat k\)
\(\overrightarrow P\) ও \(\overrightarrow Q\) এর লব্ধি ভেক্টরের সমান্তরাল একক ভেক্টর \(=\frac{\overrightarrow R}{\left|\overrightarrow R\right|}=\frac{\overrightarrow P+\overrightarrow Q}{\left|\overrightarrow P+\overrightarrow Q\right|}\)
১। \(\overrightarrow A=2\widehat i-2\widehat j+\widehat k\) ভেক্টরটির মান কত ?
২। \(\overrightarrow P=6\widehat i-3\widehat j+2\widehat k\) ভেক্টরটির দিক বা অভিমুখ নির্ণয় কর ?
৩। \(\overrightarrow P=4\widehat i-3\widehat j\) ভেক্টরটির সমান্তরাল একক ভেক্টর নির্ণয় কর ?
৪। ত্রিমাত্রিক স্থানাঙ্ক ব্যবস্থায় A(2,3,-1) এবং B(5,-6,7) দুইটি বিন্দু হলে, AB বাহুর দৈর্ঘ্য নির্ণয় কর।
৫। দুইটি ভেক্টর \(\overrightarrow P=6\widehat i-3\widehat j+2\widehat k\) এবং \(\overrightarrow Q=2\widehat i-2\widehat j-\widehat k\) । এমন একটি ভেক্টর নির্ণয় কর, যার মান এর মানের সমান এবং যার দিক এর সমান্তরাল ।
১। \(\overrightarrow A=2\widehat i-2\widehat j+\widehat k\) ভেক্টরটির মান কত ?
সমাধান
\(\overrightarrow A\) এর মান, \(\left|\overrightarrow A\right|=\sqrt{2^2+{(-2)}^2+1^2}=3\) একক
২। \(\overrightarrow P=6\widehat i-3\widehat j+2\widehat k\) ভেক্টরটির দিক বা অভিমুখ নির্ণয় কর ?
সমাধান
\(\overrightarrow P\) এর দিক বা অভিমুখ, \(\widehat p=\frac{\overrightarrow P}{\left|\overrightarrow P\right|}=\frac{6\widehat i-3\widehat j+2\widehat k}{\sqrt{6^2+{(-3)}^2+2^2}}=\frac{6\widehat i-3\widehat j+2\widehat k}7\)
৩। \(\overrightarrow P=4\widehat i-3\widehat j\) ভেক্টরটির সমান্তরাল একক ভেক্টর নির্ণয় কর ?
সমাধান
\(\overrightarrow P\) ভেক্টরটির সমান্তরাল একক ভেক্টর, \(\widehat p=\frac{\overrightarrow P}{\left|\overrightarrow P\right|}=\frac{4\widehat i-3\widehat k}{\sqrt{4^2+{(0)}^2+{(-3)}^2}}=\frac{4\widehat i-3\widehat k}5\)
৪। ত্রিমাত্রিক স্থানাঙ্ক ব্যবস্থায় A(2,3,-1) এবং B(5,-6,7) দুইটি বিন্দু হলে, AB বাহুর দৈর্ঘ্য নির্ণয় কর।
সমাধান
AB বাহু ভেক্টর, \(\overrightarrow{AB}=\overrightarrow B-\overrightarrow A=\left(5\widehat i-6\widehat j+7\widehat k\right)-\left(2\widehat i+3\widehat j-\widehat k\right)=3\widehat i-9\widehat j+8\widehat k\)
AB বাহুর দৈর্ঘ্য, \(AB=\left|\overrightarrow{AB}\right|=\sqrt{3^2+{(-9)}^2+8^2}=\sqrt{154}\) একক
৫। দুইটি ভেক্টর \(\overrightarrow P=6\widehat i-3\widehat j+2\widehat k\) এবং \(\overrightarrow Q=2\widehat i-2\widehat j-\widehat k\) । এমন একটি ভেক্টর নির্ণয় কর, যার মান এর মানের সমান এবং যার দিক এর সমান্তরাল ।
সমাধান
ভেক্টর রাশি = মান \(\times\) দিক
সুতরাং ভেক্টর রাশিটি, \(\overrightarrow A=\left|\overrightarrow P\right|\times\widehat q=\sqrt{6^2+\left(-3\right)^2+2^2}\times\frac{2\widehat i-2\widehat j-\widehat k}{\sqrt{2^2+\left(-2\right)^2+\left(-1\right)^2}}=\frac73\left(2\widehat i-2\widehat j-\widehat k\right)\)
টপিকস - 2.3: বিশেষ ভেক্টর ।
বিশেষ ভেক্টর
ভেক্টর রাশির মধ্যে বিশেষ কিছু ভেক্টর আছে যাদের বিভিন্ন নামে ডাকা হয় । যেমন-
অবস্থান ভেক্টরঃ প্রসঙ্গ কাঠামোর মূল বিন্দুর সাপেক্ষে কোন বিন্দুর অবস্থান যে ভেক্টরের সাহায্যে নির্ণয় বা নির্দেশ করা হয় তাকে অবস্থান ভেক্টর বলে । একে ব্যাসার্ধ ভেক্টর ও বলা হয় । একে \(\overrightarrow r\) দ্বারা প্রকাশ করা হয় ।
নাল বা শূন্য ভেক্টরঃ যে ভেক্টর রাশির মান শূন্য, তাকে নাল বা শূন্য ভেক্টর বলে । মূলত এর পাদবিন্দু ও শীর্ষবিন্দু একই । একে \(\overrightarrow 0\) দ্বারা প্রকাশ করা হয় ।
সরণ ভেক্টরঃ সরল পথে কোন নির্দিষ্ট দিকে কোন বিন্দুর অতিক্রান্ত দূরত্বকে সরণ ভেক্টর বলে । একে \(\overrightarrow r\) দ্বারা প্রকাশ করা হয় ।
সদৃশ ভেক্টরঃ সমজাতীয় সমান বা অসমান মানের দুটি ভেক্টর যদি একই দিকে ক্রিয়াশীল হয় তবে এদেরকে সদৃশ ভেক্টর বলে ।
বিপ্রতীপ ভেক্টরঃ দুইটি সমান্তরাল ভেক্টরের যদি একটির মান অপরটির বিপ্রতীপ হয় তবে তাদেরকে পরস্পরের বিপ্রতীপ ভেক্টর বলে ।
সমরেখ ভেক্টরঃ দুই বা ততোধিক ভেক্টর যদি একই রেখায় বা সমান্তরালে ক্রিয়া করে তবে তাদেরকে সমরেখ ভেক্টর বলে ।
সমতলীয় ভেক্টরঃ দুই বা ততোধিক ভেক্টর যদি একই সমতলে অবস্থান করে তবে তাদেরকে বলা হয় সমতলীয় ভেক্টর ।
আয়ত একক ভেক্টরঃ ত্রিমাত্রিক স্থানাঙ্ক ব্যবস্থায় X, Y এবং Z অক্ষ বরাবর যে তিনটি একক ভেক্টর যথাক্রমে \(\widehat i\), \(\widehat j\) এবং \(\widehat k\) বিবেচনা করা হয় তাকে আয়ত একক ভেক্টর বলে ।
একক ভেক্টরঃ যে ভেক্টরের মান এক একক তাকে একক ভেক্টর বলে । একক ভেক্টর প্রকাশের জন্য উক্ত ভেক্টরের ছোট হাতের অক্ষরের উপর ভেক্টর চিহ্ন না দিয়ে ক্যাপ (“^”) চিহ্ন ব্যবহার করা হয় ।
লব্ধিঃ দুই বা ততোধিক ভেক্টর রাশি যোগ করলে এদের ক্রিয়ায় যে নতুন ভেক্টর পাওয়া যায় তাকে লব্ধি বলে । যেমনঃ \(\overrightarrow A\) ও \(\overrightarrow B\) দুইটি ভেক্টর হলে এদের লব্ধি হবে, \(\overrightarrow R=\overrightarrow A+\overrightarrow B\)
১। সমরেখ ভেক্টরের ক্ষেত্রে ?
(ক) মান সমান (খ) দিক একই বা বিপরীত দিকে (গ) মান ও দিক সমান (ঘ) দিক লম্ব দিকে
২। কোন ভেক্টরের আদি বিন্দু এবং শেষ বিন্দু একই বিন্দুতে ?
(ক) একক ভেক্টরের (খ) অশুন্য ভেক্টরের (গ) সমতলীয় ভেক্টরের (ঘ) নাল ভেক্টরের
১।খ ২।ঘ
টপিকস - 2.4: ভেক্টর রাশির যোগের সূত্র, ত্রিমাত্রিক ভেক্টরের মান ও দিক, ত্রিমাত্রিক ভেক্টরের যোগ বিয়োগ ।
ভেক্টর রাশির যোগের সূত্র
মানের সাথে দিক জড়িত থাকায় ভেক্টর রাশির যোগ সাধারণ বীজগাণিতিক নিয়মে করা সম্ভব হয় না । দিক এ ক্ষেত্রে বিঘ্ন ঘটায় । ভেক্টর রাশির যোগ নিম্নক্ত পাঁচটি নিয়মে করা যায় । যথাঃ
১। সাধারণ সূত্র ।
২। ত্রিভুজ সূত্র ।
৩। বহুভুজ সূত্র ।
৪। সামান্তরিক সূত্র ।
৫। উপাংশ সূত্র ।
সাধারণ সূত্র
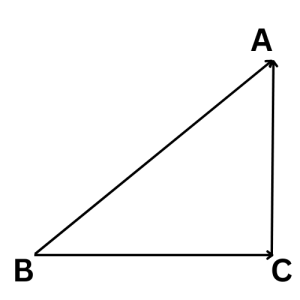
সমজাতীয় দুটি ভেক্টরের প্রথমটির শীর্ষ বিন্দু এবং দ্বিতীয়টির আদি বিন্দু একই বিন্দুতে স্থাপন করলে প্রথম ভেক্টরের আদি বিন্দু ও দ্বিতীয় ভেক্টরের শীর্ষবিন্দুর মধ্যে সংযোগকারী সরলরেখার দিকে লব্ধি ভেক্টরের মান ও দিক নির্দেশ করে ।
চিত্রে,
\(\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{BA}\\\overrightarrow{BC}=\overrightarrow P\\\overrightarrow{CA}=\overrightarrow Q\\\overrightarrow{BA}=\overrightarrow R\)
হলে লব্ধি ভেক্টর, \(\overrightarrow R=\overrightarrow P+\overrightarrow Q\)
ত্রিভুজ সূত্র

দুটি ভেক্টর কোন ত্রিভুজের সন্নিহিত বাহু দ্বারা একই ক্রমে মানে ও দিকে সূচিত করা হলে ত্রিভুজের তৃতীয় বাহুটি বিপরীত ক্রমে ভেক্টর দ্বয়ের লব্ধির মান ও দিক নির্দেশ করে ।
চিত্রে,
\(\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{BA}\\\overrightarrow{BC}=\overrightarrow P\\\overrightarrow{CA}=\overrightarrow Q\\\overrightarrow{BA}=\overrightarrow R\)
হলে লব্ধি ভেক্টর, \(\overrightarrow R=\overrightarrow P+\overrightarrow Q\)
আবার,
\(\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{BA}\\\overrightarrow{BC}+\overrightarrow{CA}=-\overrightarrow{BA}\\\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}=0\)
অর্থাৎ ত্রিভুজের তিনটি বাহুকে একই ক্রমে নির্দেশ করলে বলা যায় লব্ধি শূন্য ।
বহুভুজ সূত্র
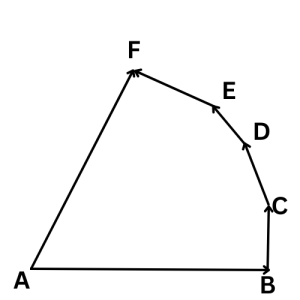
একটি বহুভুজের সবগুলো বাহুকে একই ক্রমে কতগুলো ভেক্টর দ্বারা নির্দেশ করলে শেষোক্ত বাহুটি বিপরিতক্রমে এদের লব্ধির মান ও দিক নির্দেশ করবে ।
চিত্রে,
\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EF}=\overrightarrow{AF}\\\overrightarrow{AB}=\overrightarrow a,\;\overrightarrow{BC}=\overrightarrow b,\;\overrightarrow{CD}=\overrightarrow c,\;\overrightarrow{DE}=\overrightarrow d,\;\overrightarrow{EF}=\overrightarrow e,\;\overrightarrow{AF}=\overrightarrow R\)
হলে লব্ধি ভেক্টর, \(\overrightarrow R=\overrightarrow a+\overrightarrow b+\overrightarrow c+\overrightarrow d+\overrightarrow e\)
সামান্তরিক সূত্র
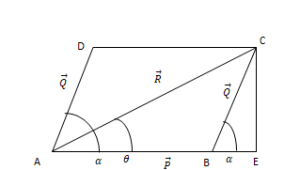
কোন সামান্তরিকের যেকোনো দুইতি সন্নিহিত বাহু যদি কোন কণার উপর একই সময়ে ক্রিয়ারত দুটি ভেক্টর রাশির মান ও দিক নির্দেশ করে, তবে ঐ বিন্দু হতে অঙ্কিত সামান্তরিকের কর্ণই এদের লব্ধির মান ও দিক নির্দেশ করবে ।
চিত্রে,
সামান্তরিক সূত্রানুসারে, \(\overrightarrow R=\overrightarrow P+\overrightarrow Q\)
এখন, BEC ত্রিভুজে,
\(BE=BC\times\cos\alpha\)
\(CE=BC\times\sin\alpha\)
ACE সমকোণী ত্রিভুজে,
\(AC^2=\left(AB^2+BE^2\right)+CE^2=AB^2+BE^2+CE^2+2AB\times BE\\AC^2=AB^2+BE^2+CE^2+2AB\times BC\times\cos\alpha\\R=\sqrt{P^2+Q^2+2PQ\;\cos\alpha}\)
লব্ধি, \(R=\sqrt{P^2+Q^2+2PQ\;\cos\alpha}\)
লব্ধির দিক \(\overrightarrow P\) এর সাথে \(\theta\) কোণে হলে, \(\tan\theta=\frac{CE}{AB+BE}=\frac{Q\sin\alpha}{P+Q\cos\alpha}\)
তাহলে, \(\overrightarrow R=\overrightarrow P+\overrightarrow Q\) এর থেকে-
লব্ধির মান, \(R=\sqrt{P^2+Q^2+2PQ\;\cos\alpha}\)
লব্ধির দিক \(\overrightarrow P\) এর সাথে \(\theta\) কোণে হলে, \(\tan\theta=\frac{Q\sin\alpha}{P+Q\cos\alpha}\)
বিশেষ ক্ষেত্র
\(R=\sqrt{P^2+Q^2+2PQ\;\cos\alpha}\) সূত্রে \(\cos\alpha\) এর মান বাড়তে থাকলে R এর মানও বাড়তে থাকবে । সুতরাং \(\cos\alpha\) এর মান সর্বোচ্চ হলে R এর মানও সর্বোচ্চ হবে । \(\cos\alpha\) এর সর্বোচ্চ মান 1, যখন \(\alpha=0^o\)
- \(\alpha=0^o\) হলে, \(R=R_{max}\)
\(R_{max}=\sqrt{P^2+Q^2+2PQ\cos0^o}=P+Q\\R_{max}=P+Q\)
\(R=\sqrt{P^2+Q^2+2PQ\;\cos\alpha}\) সূত্রে \(\cos\alpha\) এর মান কমতে থাকলে R এর মানও কমতে থাকবে । সুতরাং \(\cos\alpha\) এর মান সর্বনিম্ন হলে R এর মানও সর্বনিম্ন হবে । \(\cos\alpha\) এর সর্বনিম্ন মান -1, যখন \(\alpha=180^o\)
- \(\alpha=180^o\) হলে, \(R=R_{min}\)
\(R_{min}=\sqrt{P^2+Q^2+2PQ\cos0^18o}=P-Q\\R_{min}=P-Q\)
- \(\alpha=90^o\) হলে, \(R=R_{90}\)
\(R_{90}=\sqrt{P^2+Q^2+2PQ\cos0^90}=\sqrt{P^2+Q^2}\\R_{90}=\sqrt{P^2+Q^2}\)
এখন, \({R^2}_{max}+{R^2}_{min}=\left(P+Q\right)^2+\left(P-Q\right)^2=2\left(P^2+Q^2\right)=2R_{90}^2\)
\({R^2}_{max}+{R^2}_{min}=2R_{90}^2\)
তিন বলের লব্ধি শূন্য
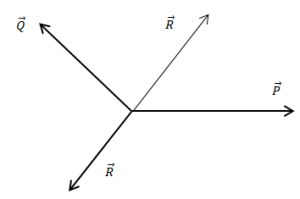
মনে করি, কোন বস্তুর উপর একইসাথে ক্রিয়ারত \(\overrightarrow P\) ও \(\overrightarrow Q\) দুইটি ভেক্টরের লব্ধি \(\overrightarrow R\) । এখন বস্তুটিকে \(\overrightarrow R\) এর ঠিক বিপরীত দিকে লব্ধির সমান বলে টেনে ধরলে বস্তুটির ক্ষেত্রে কি ঘটবে ?
নিশ্চয়ই বস্তুটি স্থির হয়ে যাবে বা সাম্যবস্থায় থাকবে । তবে শর্ত হল- \(\overrightarrow P\) ও \(\overrightarrow Q\) এর লব্ধি \(\overrightarrow R\) হতে হবে । এই একটি শর্ত পুর্ণ করলে আমরা বলতে পারবো, এখানে যেকোন দুইটি ভেক্টরের লব্ধি তৃতীয়টি হবে । অর্থাৎ-
\(\overrightarrow P\) ও \(\overrightarrow Q\) এর লব্ধি \(\overrightarrow R\) হবে ।
\(\overrightarrow Q\) ও \(\overrightarrow R\) এর লব্ধি \(\overrightarrow P\) হবে ।
\(\overrightarrow R\) ও \(\overrightarrow Q\) এর লব্ধি \(\overrightarrow P\) হবে ।
উপাংশ সূত্র
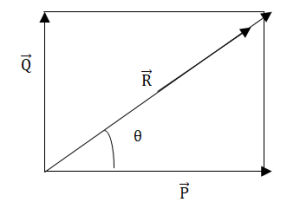
ভেক্টর রাশিকে দুই বা ততোধিক ভেক্টর রাশিতে বিভক্ত করা যায় । এই বিভক্ত অংশগুলোকে মূল ভেক্টর রাশির অংশক বা উপাংশ বলে ।
চিত্রটি হতে, \(\frac P{\cos\alpha}=\frac Q{\sin\alpha}=\frac R{\sin90^o}=R\)
সুতরাং,
আনুভূমিক উপাংশ, \(P=R\cos\alpha\)
এবং উলম্ব উপাংশ, \(Q=R\sin\alpha\)
যখন P ও Q উপাংশ দুটিকে R এর লম্বাংশ বলে ।
মনে রাখবেঃ যার সাথে আছে, তার সাথে । যার সাথে নাই, তার সাথে হবে ।
লম্বাংশ বা উপাংশের সাহায্যে কিছু ঘটনার ব্যাখ্যা করা যায়
১। নৌকার গুণ টানা ।
২। ঘোড়ার গাড়ি টানা ।
৩। লন-রোলার ঠেলা অপেক্ষা টানা সহজতর ।
৪। বেলচা দিয়ে বালি উঠানো সহজ ।
১। পরস্পর \(120^o\) কোণে ক্রিয়ারত দুইটি ভেক্টরের মান 12 একক এবং 6 একক । এদের লব্ধির মান ও দিক নির্ণয় কর ।
২। প্রমাণ কর যে, দুইটি সমান ভেক্টরের লব্ধি তাদের মধ্যবর্তী কোণকে সমদ্বিখণ্ডিত করে ?
৩। দুইটি ভেক্টরের লব্ধির সর্বোচ্চ মান 20 এবং সর্বনিম্ন মান 15 । এখন ভেক্টর দুইটি পরস্পর লম্ব বরাবর ক্রিয়া করলে এদের লব্ধির মান কত হবে ?
১। পরস্পর \(120^o\) কোণে ক্রিয়ারত দুইটি ভেক্টরের মান 12 একক এবং 6 একক । এদের লব্ধির মান ও দিক নির্ণয় কর ।
সমাধান
ধরি, P=12 একক এবং Q=6 একক । এদের মধ্যবর্তী কোণ, \(\alpha=120^o\)
লব্ধির মান, \(R=\sqrt{P^2+Q^2+2PQ\;\cos\alpha}=\sqrt{12^2+6^2+2\times12\times6\times\;\cos120^o}=6\sqrt3\) একক
লব্ধির দিক- 12 একক এর সাথে \(\theta\) কোণে হলে,
\(\tan\theta=\frac{Q\sin\alpha}{P+Q\cos\alpha}=\frac{6\times\sin120^o}{12+6\times\cos120^o}=\frac1{\sqrt3}\\\theta=30^o\)
২। প্রমাণ কর যে, দুইটি সমান ভেক্টরের লব্ধি তাদের মধ্যবর্তী কোণকে সমদ্বিখণ্ডিত করে ?
সমাধান
মনে করি, সমান ভেক্টর দুইটির মান P এবং P । এদের মধ্যবর্তী কোন \(\alpha\ এবং লব্ধি P এর সাথে \(\theta\ কোণে আছে ।
তাহলে,
\(\tan\theta=\frac{P\sin\alpha}{P+P\cos\alpha}=\frac{P\times2\times\sin{\displaystyle\frac\alpha2}\times\cos{\displaystyle\frac\alpha2}}{P\times2\times\cos^2{\displaystyle\frac\alpha2}}=\tan\frac\alpha2\\\theta=\frac\alpha2\)
৩। দুইটি ভেক্টরের লব্ধির সর্বোচ্চ মান 20 এবং সর্বনিম্ন মান 15 । এখন ভেক্টর দুইটি পরস্পর লম্ব বরাবর ক্রিয়া করলে এদের লব্ধির মান কত হবে ?
সমাধান
(Rmax)2 + (Rmin)2 = 2.(R90)2
বা, \(20^2+15^2=2\times R_{10}^2\\R_{90}=\frac{25}{\sqrt2}\)
টপিকস - 2.5: উপাংশের সূত্রের সাহায্যে বাস্তব ঘটনার ব্যাখ্যা ।
১। নৌকার গুণ টানা
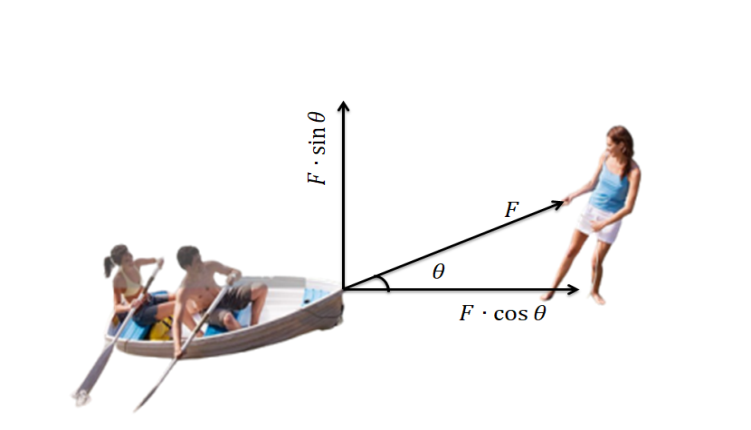
এক্ষেত্রে নৌকায় একটি রশি বেঁধে নদীর কিনারা থেকে টানা হয় । কিভাবে নৌকাটি হালকা মনে হয় এবং সামনে চলে আসে, তা উপাংশ সূত্রের মাধ্যমে ব্যাখ্যা করা যায় ।
নৌকাটিকে F বলে টানা হলে এটি \(F\cos\theta\) এবং \(F\sin\theta\) এই দুইটি উপাংশে আনুভূমিক এবং উলম্বদিকে বিভক্ত হয় ।
\(F\cos\theta\) : নৌকাটিকে সামনের দিকে নিয়ে যায় ।
\(F\sin\theta\) : নৌকাটির ওজনের বিপরীতে কাজ করে নৌকার ওজন কমিয়ে দেয় ।
নৌকার অনুভূত ওজন : \(mg-F\sin\theta\)
এখানে \(\theta\) এর মান কমলে \(F\cos\theta\) এর মান বাড়বে এবং \(F\sin\theta\) এর মান কমবে । ফলে নৌকা দ্রুত সামনের দিকে যাবে এবং নৌকাটি আগের চেয়ে বেশি ভারি বলে মনে হবে ।
২। ঘোড়ার গাড়ি টানা
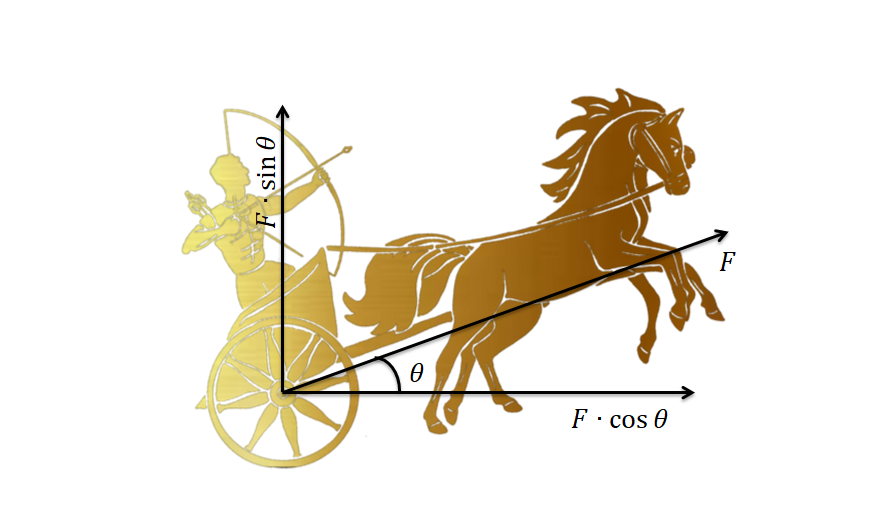
এক্ষেত্রে ঘোড়ার গাড়িতে একটি রশি বা লাঠি বেঁধে তা ঘোড়ার কাঁধে বেঁধে দেওয়া হয় । কিভাবে গাড়িটি হালকা মনে হয় বা লাফায় এবং গাড়িটি সামনে চলে আসে, তা উপাংশ সূত্রের মাধ্যমে ব্যাখ্যা করা যায় ।
গাড়িটিকে F বলে টানা হলে এটি \(F\cos\theta\) এবং \(F\sin\theta\) এই দুইটি উপাংশে আনুভূমিক এবং উলম্বদিকে বিভক্ত হয় ।
\(F\cos\theta\) : ঘোড়ার গাড়িকে সামনের দিকে নিয়ে যায় ।
\(F\sin\theta\) : গাড়ির ওজনের বিপরীতে কাজ করে গাড়ির ওজন কমিয়ে দেয় এবং গাড়িটি লাফায় ।
গাড়ির অনুভূত ওজন : \(mg-F\sin\theta\)
এখানে \(\theta\) এর মান কমলে \(F\cos\theta\) এর মান বাড়বে এবং \(F\sin\theta\) এর মান কমবে । ফলে গাড়ি দ্রুত সামনের দিকে যাবে এবং গাড়িটি আগের চেয়ে বেশি ভারি বলে মনে হবে । সেই সাথে ঘোড়ার গাড়িটি কম লাফাবে ।
৩। লন-রোলার বা লাগেজ ঠেলা অপেক্ষা টানা সহজতর
ঠেলার ক্ষেত্রে
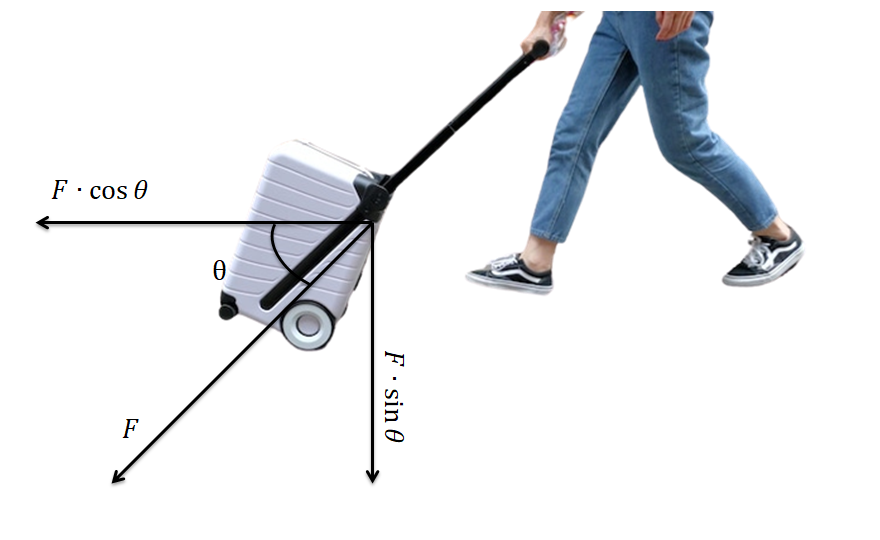
লাগেজের হাতল ধরে ঠেলার ক্ষেত্রে আমরা হাতলের মাধ্যমে লাগেজে বল প্রয়োগ করি । এখানে হাতলের মাধ্যমে লাগেজে F বল প্রয়োগ করা হলে এটি \(F\cos\theta\) এবং \(F\sin\theta\) এই দুইটি উপাংশে আনুভূমিক এবং খাড়া নিচের দিকে বিভক্ত হয় ।
\(F\cos\theta\) : লাগেজকে সামনের দিকে নিয়ে যায় ।
\(F\sin\theta\) : লাগেজের ওজনের দিকে ক্রিয়া করে লাগেজের ওজন বাড়িয়ে দেয় ।
লাগেজের অনুভূত ওজন : \(mg+F\sin\theta\)
ফলে লাগেজ ঠেলা হলে লাগেজ ভারি বলে মনে হয় । তাই ঠেলে নিয়ে যেতে বেশি কষ্ট হয় ।
টানার ক্ষেত্রে
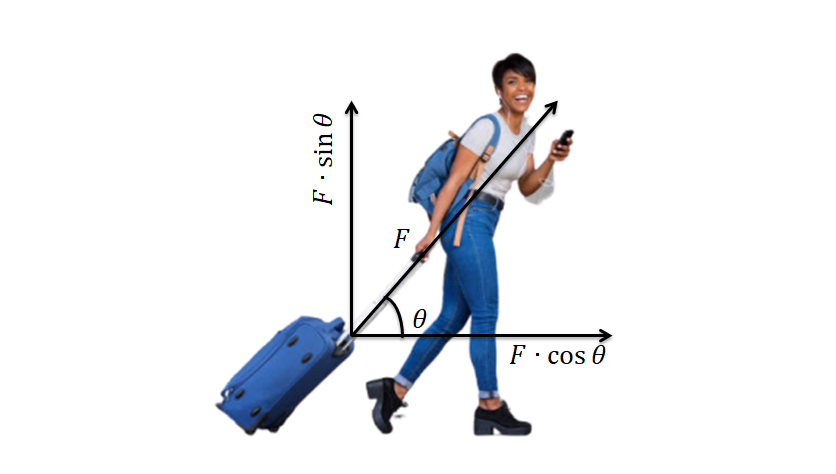
লাগেজের হাতল ধরে টানার সময় আমরা হাতলের মাধ্যমে লাগেজকে টানি । এখানে হাতলের মাধ্যমে লাগেজে F বল প্রয়োগ করা হলে এটি \(F\cos\theta\) এবং \(F\sin\theta\) এই দুইটি উপাংশে আনুভূমিক এবং উলম্বদিকে বিভক্ত হয় ।
\(F\cos\theta\) : লাগেজকে সামনের দিকে নিয়ে যায় ।
\(F\sin\theta\) : লাগেজের ওজনের বিপরীতে ক্রিয়া করে লাগেজের ওজন কমিয়ে দেয় ।
লাগেজের অনুভূত ওজন : \(mg-F\sin\theta\)
ফলে লাগেজ টানা হলে লাগেজ হালকা বলে মনে হয় । তাই টেনে নিয়ে যেতে পরিশ্রম কম হয় ।
উল্লেখিত কারণে লন রোলার বা লাগেজ ঠেলা অপেক্ষা টানা সহজতর ।
৪। বেলচা দিয়ে বালি ওঠানো
কোদালা ব্যবহার করা হলে

কোদালা দিয়ে বালি ওঠানোর ক্ষেত্রে কোদালার হাতল ধরে উপরের দিকে টানা হয় । টানার ক্ষেত্রে হাতলের মাধ্যমে কোদালায় বল প্রয়োগ করা হয় । এখানে হাতলের মাধ্যমে কোদালায় F বল প্রয়োগ করা হলে এটি \(F\cos\theta\) এবং \(F\sin\theta\) এই দুইটি উপাংশে আনুভূমিক এবং উলম্বদিকে বিভক্ত হয় ।
\(F\cos\theta\) : কোদালাকে সামনের দিকে বা বালির ভিতর থেকে বাইরে নিয়ে আসে ।
\(F\cos\theta\) : কোদালার ওজনের বিপরীত দিকে ক্রিয়া করে কোদালার ওজন কমিয়ে দেয় । আর এই ওজন কমে মূলত কোদালার উপর কম বালি ঊঠে আসার মাধ্যমে ।
কোদালার উপর বালির ওজন : \(mg-F\sin\theta\)
এক্ষেত্রে যেহেতু কোদালায় কম পরিমাণ বালি উঠছে, তাই বালি ওঠানোর জন্য অনেক সময়ের প্রয়োজন হবে ।
বেলচা ব্যবহার করা হলে

বেলচা দিয়ে বালি ওঠানোর ক্ষেত্রে বেলচার হাতল ধরে নিচের দিকে ঠেলা হয় । ঠেলার ক্ষেত্রে হাতলের মাধ্যমে বেলচায় বল প্রয়োগ করা হয় । এখানে হাতলের মাধ্যমে বেলচায় F বল প্রয়োগ করা হলে এটি \(F\cos\theta\) এবং \(F\sin\theta\) এই দুইটি উপাংশে আনুভূমিক এবং খাড়া নিচের দিকে বিভক্ত হয় ।
\(F\cos\theta\) : বেলচাকে সামনের দিকে বা বালির ভিতরের দিকে নিয়ে যায় ।
\(F\cos\theta\) : বেলচার ওজনের দিকে ক্রিয়া করে বেলচার ওজন বাড়িয়ে দেয় । আর এই ওজন বাড়ে মূলত বেলচার উপর বেশি বালি ঊঠে আসার মাধ্যমে ।
বেলচার উপর বালির ওজন : \(mg+F\sin\theta\)
এক্ষেত্রে যেহেতু বেলচায় বেশি পরিমাণ বালি উঠছে, তাই কম সময়েই অধিক বালি ওঠানো যাবে।
উল্লেখিত কারণে বালি ওঠানোর জন্য কোদালা ব্যবহার না করে বেলচা ব্যবহার করা হয় ।
টপিকস - 2.6: ভেক্টর যোগের সামান্তরিক সূত্রের ব্যবহার ।
ভেক্টর যোগের সামান্তরিক সূত্রের ব্যবহার
ভেক্টর যোগের সামান্তরিক সূত্র ব্যবহার করে অনেক বাস্তব ঘটনা ব্যাখ্যা করা হয় । এই অধ্যায়ে যা করা হবে –
১। নৌকা নদী সংক্রান্ত ।
২। বৃষ্টিতে ছাতা ধরা সংক্রান্ত ।
৩। বৃষ্টিতে গাড়ির কাঁচ ভেজা সংক্রান্ত ।
৪। আপেক্ষিক বেগ ।
টপিকস - 2.7: নৌকা নদী সংক্রান্ত সমস্যা ।
ক। সোজাসুজি বা লম্বালম্বি বা আড়াআড়ি ভাবে বা সর্বনিম্ন দূরত্বে নদী পার
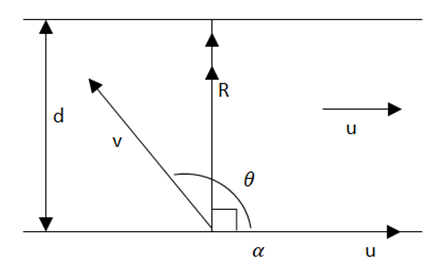
লব্ধি স্রোতের সাথে লম্ব ভাবে \(\left(\theta=90\right)\) হবে এবং নৌকা স্রোতের সাথে \(90^o\) অপেক্ষা বেশি (\(\left(\alpha>90^o\right)\) কোণে চালনা করতে হবে । এরূপ শর্তে – যখন স্রোতের বেগ u , নৌকার বেগ v, নদীর প্রস্থ d , নদী পারাপারের প্রয়োজনীয় সময় t এবং লব্ধি বেগ R ।
এখানে,
জানা আছে–
\(\theta=90^o\)
প্রশ্ন করা যেতে পারে–
নদী পার হওয়ার জন্য কোন দিকে রওনা দিতে হবে, \(\alpha=?\)
লব্ধি বেগ কত, \(R=?\)
নদী পার হতে কত সময় লাগবে, \(t=?\)
নদীর প্রস্থ কত, \(d=?\)
এখানে,
\(\tan\theta=\tan90^o=\frac10=\frac{v\;\sin\alpha}{u+v\;\cos\alpha}\)
বা, \(u+v\;\cos\alpha=0\)
বা, \(v\;\cos\alpha=-u\)
\(\alpha=\cos^{-1}\left(-\frac uv\right)\)
লব্ধির বেগ,
\(R=\sqrt{u^2+v^2+2uv\;\cos\alpha}\)
\(R=\sqrt{u^2+v^2+2u(-u)}\) [\(v\;\cos\alpha=-u\)]
\(R=\sqrt{v^2-u^2}\)
\(R=\sqrt{v^2-v^2\cos^2\alpha}=v\;\sin\alpha\)
নদীর প্রস্থ বরাবর নৌকা এবং স্রোতের বেগের উপাংশ,
\(R=u\;\cos90^o+v\;\cos\left(\alpha-90^o\right)=v\;\cos\left(90^o-\alpha\right)=v\;\sin\alpha\)
সুতরাং, \(R=\sqrt{v^2-u^2}=v\;\sin\alpha\)
নদী পার হওয়ার জন্য প্রয়োজনীয় সময়,
\(t=\frac dR=\frac d{\sqrt{v^2-u^2}}=\frac d{v\;\sin\alpha}\)
লক্ষনীয়,
\(\alpha=\cos^{-1}\left(-\frac uv\right)\)
এখানে নৌকার বেগ স্রোতের বেগের দিগুণ হলে, \(\alpha=\cos^{-1}\left(-\frac u{2u}\right)=\cos^{-1}\left(-\frac12\right)=120^o\)
যেহেতু স্রোতের বেগ নৌকার বেগের দিগুণ হলে এখানে অসঙ্গায়িত আসে, তাই বলা যেতে পারে- দিগুণ কথা উল্লেখ থাকলে উত্তর \(120^o\) ।
লক্ষনীয়,
এখানে \(\sin\alpha\) এর মান বাড়তে থাকলে t এর মান কমতে থাকবে । কাজেই \(\sin\alpha\) এর মান সর্বোচ্চ হলে t এর মান সর্বনিম্ন হবে ।
যেহেতু \(\sin\alpha\) এর সর্বোচ্চ মান 1, যখন \(\alpha=90^o\) । তাই এর সর্বনিম্ন মান হবে \(t=\frac dv\) ।
অর্থাৎ \(\alpha=90^o\) কোণে বা লম্বালম্বি রওনা দিলে নদীটি সর্বনিম্ন সময়ে পাড়ি দেওয়া সম্ভব । যা আমরা এর পরের বিষয়ে পড়ব ।
খ। সোজাসুজি বা লম্বালম্বি যাত্রা করে অথবা সর্বনিম্ন সময়ে নদী পার
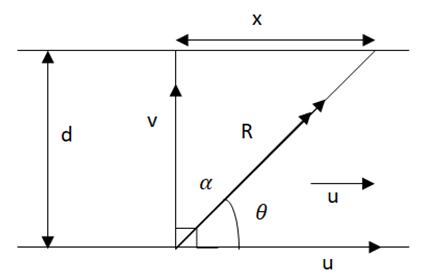
লব্ধি স্রোতের সাথে \(90^o\) অপেক্ষা কম কোণে \(\left(\theta<90^o\right)\) এবং নৌকা স্রোতের সাথে \(\alpha=90^o\) কোণে চালনা করতে হবে । এরূপ শর্তে – যখন স্রোতের বেগ u , নৌকার বেগ v , নদীর প্রস্থ d , নদী পারাপারের প্রয়োজনীয় সময় t লব্ধি বেগ এবং প্রস্থ বরাবর সরণ x ।
এখানে,
জানা আছে–
\(\alpha=90^o\)
প্রশ্ন করা যেতে পারে–
লব্ধির দিক নির্ণয় কর, \(\theta=?\)
লব্ধি বেগ কত, \(R=?\)
নদী পার হতে কত সময় লাগবে, \(t=?\)
নদীর প্রস্থ কত, \(d=?\)
নদীর প্রস্থ বরাবর বা আনুভূমিক সরণ কত, \(x=?\)
এখানে,
\(\tan\theta=\frac{v\;\sin\alpha}{u+v\;\cos\alpha}=\frac{v\;\sin90^o}{u+v\;\cos90^o}=\frac vu\)
লব্ধির বেগ,
\(R=\sqrt{u^2+v^2+2uv\;\cos\alpha}\)
\(R=\sqrt{u^2+v^2+2uv\;\cos90^o}=\sqrt{u^2+v^2}\)
নদী পার হওয়ার জন্য প্রয়োজনীয় সময়,
\(t=\frac d{v\;\sin\alpha}=\frac d{v\;\sin90^o}=\frac dv\)
\(t=t_{min}=\frac dv\)
সমকোণী ত্রিভুজ ব্যবহার করে,
\(\tan\theta=\frac dx\)
সুতরাং, \(\frac vu=\frac dx\)
গ। কম সময়ে নদী পার
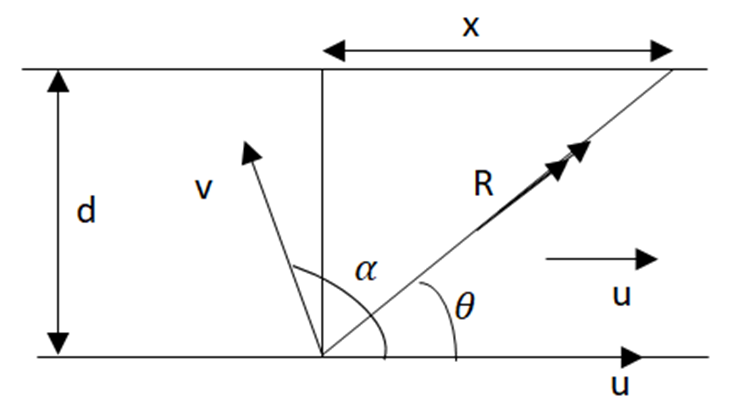
লব্ধি স্রোতের সাথে \(90^o\) অপেক্ষা কম কোণে \(\left(\theta<90^o\right)\) এবং নৌকা স্রোতের সাথে \(\theta\) অপেক্ষা বেশি \(\alpha>\theta\) কোণে চালনা করতে হবে । এরূপ শর্তে – যখন স্রোতের বেগ u , নৌকার বেগ v , নদীর প্রস্থ d , নদী পারাপারের প্রয়োজনীয় সময় t লব্ধি বেগ R এবং প্রস্থ বরাবর সরণ x ।
এখানে,
প্রশ্ন করা যেতে পারে–
নদী পার হওয়ার জন্য কোন দিকে রওনা দিতে হবে, \(\alpha=?\)
লব্ধির দিক নির্ণয় কর, \(\theta=?\)
লব্ধি বেগ কত, \(R=?\)
নদী পার হতে কত সময় লাগবে, \(t=?\)
নদীর প্রস্থ কত, \(d=?\)
নদীর প্রস্থ বরাবর বা আনুভূমিক সরণ কত, \(x=?\)
এখানে,
লব্ধি বেগ,
\(R=\sqrt{u^2+v^2+2uv\;\cos\alpha}\)
লব্ধির দিক,
\(\tan\theta=\frac{v\;\sin\alpha}{u+v\;\cos\alpha}\)
নদীর প্রস্থ বরাবর নৌকা এবং স্রোতের বেগের উপাংশ,
\(w=u\;\cos90^o+v\;\cos\left(\alpha-90^o\right)=v\;\cos\left(90^o-\alpha\right)=v\;\sin\alpha\)
তাহলে নদী পার হওয়ার জন্য প্রয়োজনীয় সময়,
\(t=\frac d{v\;\sin\alpha}\)
আনুভূমিক বরাবর বেগের উপাংশ,
\(h=u+v\;\cos\alpha\)
আনুভূমিক বরাবর নৌকার সরণ,
\(x=\left(u+v\;\cos\alpha\right).t\)
১। একটি নৌকা স্রোতহীন নদীতে ঘন্টায় 12 km বেগে ছুটতে পারে । ঘন্টায় 5 km বেগের স্রোতযুক্ত নদীতে স্রোতের সাথে লম্বালম্বি যাত্রা করলে নৌকাটির লব্ধিবেগ কত হবে ?
২। 100 মিটার প্রসস্থ একটি স্রোতহীন নদী সোজাসুজি পাড়ি দিতে একজন সাঁতারুর 4 মিনিট সময় লাগে । স্রোত থাকলে ঐ একই পথ পাড়ি দিতে তার 5 মিনিট সময় লাগে । নদীতে স্রোতের বেগ কত ছিল ?
৩। 1 কিলোমিটার প্রস্থের ঘন্টায় 10 কিলোমিটার স্রোতযুক্ত একটি নদী ঘন্টায় সর্বোচ্চ 20 কিলোমিটার গতির নৌকা যোগে সর্বনিম্ন কত সময়ে নদীটি পাড়ি দেওয়া সম্ভব ?
১। একটি নৌকা স্রোতহীন নদীতে ঘন্টায় 12 km বেগে ছুটতে পারে । ঘন্টায় 5 km বেগের স্রোতযুক্ত নদীতে স্রোতের সাথে লম্বালম্বি যাত্রা করলে নৌকাটির লব্ধিবেগ কত হবে ?
সমাধান
লম্বালম্বি যাত্রা করার ক্ষেত্রে,
\(R=\sqrt{u^2+v^2}=\sqrt{12^2+5^2}=13\;km/h\)
২। 100 মিটার প্রসস্থ একটি স্রোতহীন নদী সোজাসুজি পাড়ি দিতে একজন সাঁতারুর 4 মিনিট সময় লাগে । স্রোত থাকলে ঐ একই পথ পাড়ি দিতে তার 5 মিনিট সময় লাগে । নদীতে স্রোতের বেগ কত ছিল ?
সমাধান
স্রোতহীন নদীতে যে বেগ পাওয়া যায়, সেটি সাঁতারুর নিজস্ব বেগ,
\(v=\frac{100}4=25\;m/min\)
স্রোতযুক্ত নদীতে যে বেগ পাওয়া যায়, সেটি লব্ধিবেগ,
\(R=\frac{100}5=20\;m/min\)
সোজাসুজি পাড়ি দেওয়ার ক্ষেত্রে,
\(R=\sqrt{v^2-u^2}\)
বা, \(R^2=v^2-u^2\)
বা, \(20^2=25^2-u^2\)
সুতরাং স্রোতের বেগ, \(u=15\;m/min\)
৩। 1 কিলোমিটার প্রস্থের ঘন্টায় 10 কিলোমিটার স্রোতযুক্ত একটি নদী ঘন্টায় সর্বোচ্চ 20 কিলোমিটার গতির নৌকা যোগে সর্বনিম্ন কত সময়ে নদীটি পাড়ি দেওয়া সম্ভব ?
সমাধান
\(t_{min}=\frac dv=\frac1{20}=0.05\;h\;=\;0.05\times60\;min=3\;min\)
টপিকস - 2.8: বৃষ্টি ছাতা ধরা সংক্রান্ত সমস্যা ।
বৃষ্টির সাথে ছাতা ধরা
এ ধরনের সমস্যা সমাধানে সমস্যাটি কার্তেসীয় স্থানাংক ব্যবস্থায় বিবেচনা করতে হয় । এতে দেখা যায় প্রথম চতূর্ভাগে ব্যক্তির বেগ এবং বৃষ্টির বেগ একই ক্রমে নির্দেশিত । তাই এ ধরণের সমস্যা সমাধানে আমরা সর্বদা বৃষ্টির প্রতিক্রিয়াকে ধরে নিয়ে হিসাব করব ।
ক। বায়ুর বাধা না থাকলে বা বৃষ্টি খাড়াভাবে পড়লে
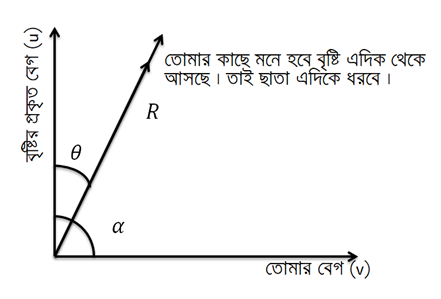
এক্ষেত্রে আমরা বৃষ্টির প্রতিক্রিয়া চিন্তা করব ।
এখানে,
\(\tan\theta=\frac{v\;\sin\alpha}{u+v\;\cos\alpha}=\frac{v\;\sin90^o}{u+v\;\cos90^o}=\frac vu\)
\(R=\sqrt{u^2+v^2+2uv\;\cos\alpha}=\sqrt{u^2+v^2+2uv\;\cos90^o}=\sqrt{u^2+v^2}\)
খ। বায়ুর বাধা থাকলে বা বৃষ্টি খাড়াভাবে না পড়লে
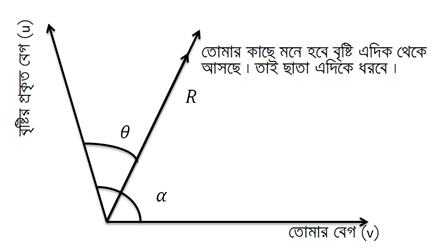
এক্ষেত্রেও আমরা বৃষ্টির প্রতিক্রিয়া চিন্তা করব ।
এখানে,
\(\tan\theta=\frac{v\;\sin\alpha}{u+v\;\cos\alpha}\)
\(R=\sqrt{u^2+v^2+2uv\;\cos\alpha}\)
১। একদিন কামাল উত্তর থেকে দক্ষিণ দিকে \(6\;kmh^{-1}\) বেগে দৌড়াচ্ছিল । তার কাছে মনে হল বৃষ্টি খাড়াভাবে \(12\;kmh^{-1}\) বেগে পড়ছে । প্রকৃত পক্ষে বৃষ্টি কোন দিক থেকে পড়ছে এবং বৃষ্টির বেগ কত ছিল ?
১। একদিন কামাল উত্তর থেকে দক্ষিণ দিকে \(6\;kmh^{-1}\) বেগে দৌড়াচ্ছিল । তার কাছে মনে হল বৃষ্টি খাড়াভাবে \(12\;kmh^{-1}\) বেগে পড়ছে । প্রকৃত পক্ষে বৃষ্টি কোন দিক থেকে পড়ছে এবং বৃষ্টির বেগ কত ছিল ?
সমাধান
এখানে,
কামালের বেগ, \(v=6\;kmh^{-1}\)
লব্ধি বেগ, \(R=12\;kmh^{-1}\) [যা মনে হয় তা লব্ধি]
আনুভূমিকের সাথে লব্ধির কোণ, \(\theta=90^o\)
বৃষ্টির প্রকৃত বেগ u এবং তা আনুভূমিকের সাথে \(\alpha\) কোণে পড়লে,
\(\tan\theta=\frac{u\;\sin\alpha}{v+u\;\cos\alpha}\)
বা, \(\tan90^o=\frac10=\frac{u\;\sin\alpha}{v+u\;\cos\alpha}\)
বা, \(v+u\;\cos\alpha=0\)
\(u\;\cos\alpha=-v\)
\(R=\sqrt{u^2+v^2+2uv\;\cos\alpha}\)
বা, \(R^2=u^2+v^2+2v(-v)\)
বা, \(R^2=u^2-v^2\)
বা, \(12^2=u^2-6^2\)
\(u=6\sqrt5\;km/h\)
আবার,
\(u\;\cos\alpha=-v\)
বা, \(6\sqrt5\;\cos\alpha=-6\)
\(\alpha=116.57^o\)
সুতরাং বৃষ্টি প্রকৃতপক্ষে \(6\sqrt5\;km/h\) বেগে আনুভূমিকের সাথে \(116.57^o\) কোণে পড়ছে ।
টপিকস - 2.9: বৃষ্টিতে গাড়ির কাঁচ ভেজা সংক্রান্ত সমস্যা।
বৃষ্টিতে গাড়ির কাঁচ ভেজা
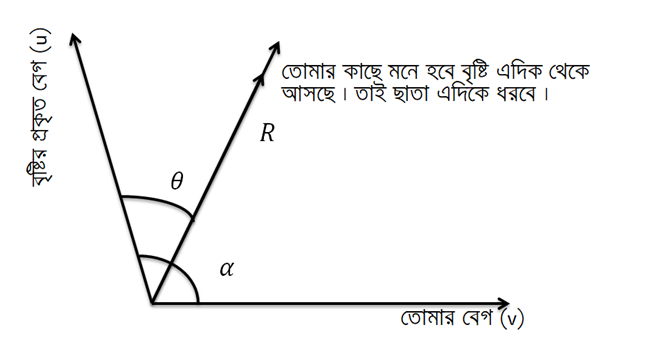
এখানে আমরা দেখেছি- প্রকৃত পক্ষে আনুভুমিকের সাথে যত কোণে বৃষ্টি পরে, আমাদের কাছে তার চেয়ে কম কোণে পড়ছে বলে মনে হয় ।
এখন আমরা যদি না দৌড়াই, তবে বৃষ্টি প্রকৃত পক্ষে যেদিক থেকে আসছে সেদিক থেকেই পড়তে দেখবো । কিন্তু আনুভূমিক দিকে আমাদের বেগ যত বাড়বে, আমাদের সাপেক্ষে বৃষ্টির আপেক্ষিক বেগ ততই আমাদের বা আনুভূমিকের দিকে চলে আসবে । বিপরীতভাবেও আমাদের বেগ যত কমবে বৃষ্টি আনুভূমিক থেকে তত দূরে সরে যাবে ।
ক। বাতাস থাকলে এবং বৃষ্টি খাড়াভাবে না পড়লে
গাড়িটির এমন গতিবেগ যার জন্য বৃষ্টি গাড়ীটিতে লম্ব ভাবে পরে, গাড়িটি সে বেগের তুলনায়-
– বেশি বেগে চললে, শুধুমাত্র সামনের কাঁচ ভিজবে ।
– কম বেগে চললে, শুধুমাত্র পিছনের কাঁচ ভিজবে ।
– সমান বেগে চললে সামন ও পিছনের উভয় কাঁচ-ই ভিজবে ।
খ। বাতাস থাকলে এবং বৃষ্টি খাড়াভাবে পড়লে
যে বেগে বাতাস প্রবাহিত হচ্ছে, গাড়িটি সে বেগের তুলনায়-
– বেশি বেগে চললে, শুধুমাত্র সামনের কাঁচ ভিজবে ।
– কম বেগে চললে, শুধুমাত্র পিছনের কাঁচ ভিজবে ।
– সমান বেগে চললে সামন ও পিছনের উভয় কাঁচ-ই ভিজবে ।
গ। বাতাস না থাকলে
এক্ষেত্রে গাড়িটি থেমে থাকলেই বৃষ্টি খাড়াভাবে পড়বে । তাই,
– গাড়িটি থেমে থাকলে সামন ও পিছনের উভয়ের কাঁচ ভিজবে ।
– সামনে চললে শুধুমাত্র সামনের কাঁচ ভিজবে ।
– পিছনে চললে শুধুমাত্র পিছনের কাঁচ ভিজবে ।
১। একদিন নোমান ঘন্টায় 50 কিলোমিটার বেগে গাড়ি চালাচ্ছিল । এই অবস্থায় তার কাছে মনে হচ্ছিল- বৃষ্টি খাড়াভাবে পড়ছে । তার কি রকম গতির জন্য গাড়ি উভয় কাঁচ, সামনের কাঁচ এবং পিছনের কাঁচ ভিজবে ?
১। একদিন নোমান ঘন্টায় 50 কিলোমিটার বেগে গাড়ি চালাচ্ছিল । এই অবস্থায় তার কাছে মনে হচ্ছিল- বৃষ্টি খাড়াভাবে পড়ছে । তার কি রকম গতির জন্য গাড়ি উভয় কাঁচ, সামনের কাঁচ এবং পিছনের কাঁচ ভিজবে ?
সমাধান
যেহেতু গাড়ির বেগ 50 km/h এর জন্য বৃষ্টি খাড়াভাবে পড়ছিল, তাই-
গাড়ির বেগ =50 km/h এর জন্য উভয় কাঁচ ভিজবে ।
গাড়ির বেগ >50 km/h এর জন্য শুধু সামনের কাঁচ ভিজবে ।
গাড়ির বেগ <50 km/h এর জন্য শুধু পিছনের কাঁচ ভিজবে ।
টপিকস - 2.10: আপেক্ষিক বেগ সংক্রান্ত সমস্যা।
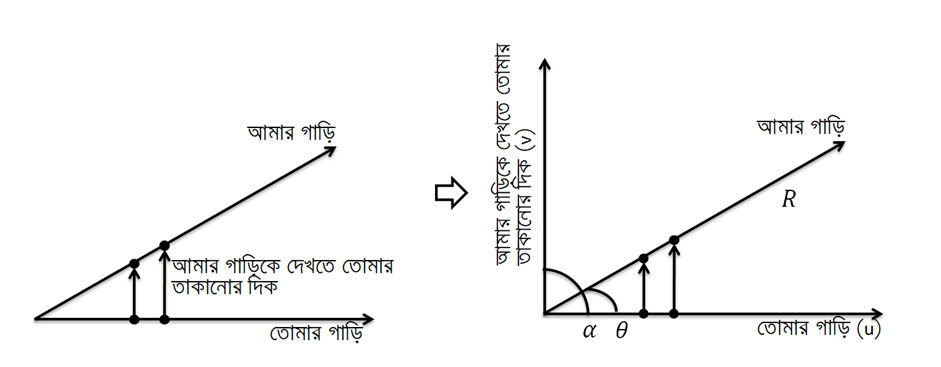
এক্ষেত্রে মূলত আমার গাড়ি প্রকৃত পক্ষে তোমার সাথে সূক্ষ্মকোণে গেলে তুমি সেটাকে আগের চেয়ে বেশি কোণে বা তোমার সাথে লম্বভাবে যেতে দেখো ।
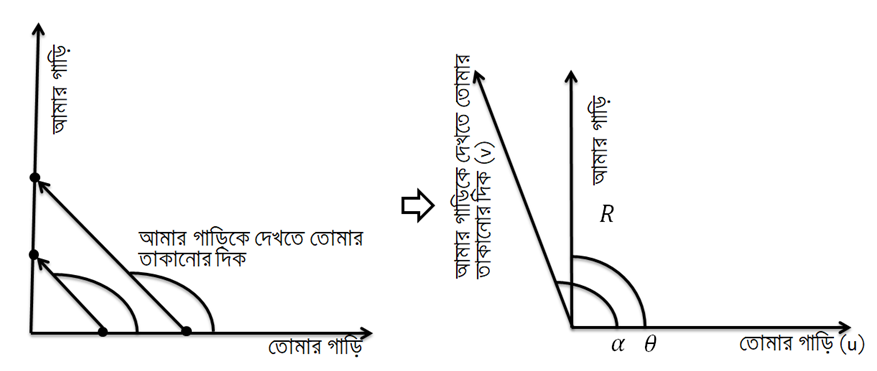
একইভাবে আমার গাড়িটি প্রকৃত পক্ষে তোমার সাথে লম্বভাবে গেলে দেখলে তুমি সেটাকে তোমার সাথে আগের চেয়ে বেশি কোণে বা স্থূলকোণে যেতে দেখবে ।
১। ঘন্টায় 40 কিলোমিটার বেগে উত্তর দিকে গতিশীল একটি ট্রাকের চালক দেখলেন একটি কার ঘন্টায় 80 কিলোমিটার বেগে \(30^o\) কোণে পশ্চিম-দক্ষিণ দিকে যাচ্ছে । প্রকৃত পক্ষে কারটি কোন দিকে যাচ্ছে?
১। ঘন্টায় 40 কিলোমিটার বেগে উত্তর দিকে গতিশীল একটি ট্রাকের চালক দেখলেন একটি কার ঘন্টায় 80 কিলোমিটার বেগে তার সাথে তথা উত্তর দিকের সাথে পশ্চিমে কোণে দূরে চলে যাচ্ছে । প্রকৃত পক্ষে কারটি কোন দিকে যাচ্ছিল?
সমাধান
\(\tan\theta=\frac{C\;\sin\alpha}{T+C\;\cos\alpha}=\frac{80\;\sin120^o}{40+80\;\cos120^o}=\frac10\)
\(\theta=90^o\)
সুতরাং কারটি প্রকৃত পক্ষে উত্তরের সাথে কোণে বা সোজা পশ্চিম দিকে যাচ্ছিল ।
টপিকস - 2.11: ভেক্টর রাশির গুণ ।
ভেক্টর রাশির গুণন
ভেক্টর রাশির গুনফল দুই প্রকার । যথাঃ ১। স্কেলার গুণন বা ডট গুণন । ২। ভেক্টর গুণন বা ক্রস গুণন ।
স্কেলার গুণন বা ডট গুণন
দুইটি ভেক্টর রাশি গুণ করলে গুনফল যদি স্কেলার রাশি হয় তবে সেই গুণনকে স্কেলার গুণন বা ডট গুণন বলে ।
\(\overrightarrow P\) ও \(\overrightarrow Q\) দুইটি ভেক্টর রাশি এবং এদের মধ্যবর্তী কোণ \(\alpha\) হলে,
স্কেলার গুনফল, \(\overrightarrow P.\overrightarrow Q=\left|\overrightarrow P\right|\times\left|\overrightarrow Q\right|\times\cos\alpha\) \(\lbrack0\leq\alpha\leq\pi\rbrack\)
এখানে, \(\overrightarrow P.\overrightarrow Q=\left|\overrightarrow P\right|\times\left|\overrightarrow Q\right|\times\cos\alpha\)
যেহেতু, \(\cos90^o=0\)
তাই \(\overrightarrow P\) ও \(\overrightarrow Q\) ভেক্টরদ্বয় পরস্পর লম্ব হলে, \(\overrightarrow P.\overrightarrow Q=0\) হবে ।
একই কারণে,
\(\widehat i.\widehat j=0\)
\(\widehat j.\widehat k=0\)
\(\widehat k.\widehat i=0\)
যেহেতু, \(\cos0^o=1\)
তাই ও ভেক্টরদ্বয় পরস্পর সমান্তরাল হলে, \(\overrightarrow P.\overrightarrow Q=\left|\overrightarrow P\right|\times\left|\overrightarrow Q\right|\) হবে ।
একই কারণে,
\(\widehat i.\widehat i=1\)
\(\widehat j.\widehat j=1\)
\(\widehat k.\widehat k=1\)
ত্রিমাত্রিক ভেক্টরের স্কেলার গুণ
মনে করি,
\(\overrightarrow A=A_x\widehat i+A_y\widehat j+A_z\widehat k\)
\(\overrightarrow B=B_x\widehat i+B_y\widehat j+B_z\widehat k\)
\(\overrightarrow A.\overrightarrow B=\left(A_x.B_x\right)+\left(A_y.B_y\right)+\left(A_z.B_z\right)\)
স্কেলার গুণন বা ডট গুণের প্রয়োগ
কাজ নির্ণয়
বল ভেক্টর \(=\overrightarrow F\) এবং সরণ ভেক্টর \(=\overrightarrow s\) হলে,
কাজ, \(W=\overrightarrow F.\overrightarrow s\)
এ জন্যই বল ও সরণ ভেক্টর রাশি হওয়া সত্ত্বেও কাজ একটি স্কেলার রাশি ।
অভিক্ষেপ এবং উপাংশ বা অংশক নির্ণয়
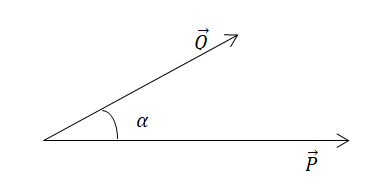
\(\overrightarrow P\) বরাবর বা \(\overrightarrow P\) এর উপর, \(\overrightarrow Q\) ভেক্টরের অভিক্ষেপ \(=\left|\overrightarrow Q\right|\cos\alpha=\frac{\overrightarrow P.\overrightarrow Q}{\left|\overrightarrow P\right|}\)
\(\overrightarrow Q\) বরাবর বা \(\overrightarrow Q\) এর উপর, \(\overrightarrow P\) ভেক্টরের অভিক্ষেপ \(=\left|\overrightarrow P\right|\cos\alpha=\frac{\overrightarrow P.\overrightarrow Q}{\left|\overrightarrow Q\right|}\)
\(\overrightarrow P\) বরাবর বা \(\overrightarrow P\) এর উপর, \(\overrightarrow Q\) ভেক্টরের উপাংশ বা অংশক \(=\left|\overrightarrow Q\right|\cos\alpha.\widehat p=\frac{\overrightarrow P.\overrightarrow Q}{\left|\overrightarrow P\right|}.\widehat p\)
\(\overrightarrow Q\) বরাবর বা \(\overrightarrow Q\) এর উপর, \(\overrightarrow P\) ভেক্টরের উপাংশ বা অংশক \(=\left|\overrightarrow P\right|\cos\alpha.\widehat q=\frac{\overrightarrow P.\overrightarrow Q}{\left|\overrightarrow Q\right|}.\widehat q\)
ভেক্টর গুণ বা ক্রস গুণ
দুইটি ভেক্টর রাশি গুণ করলে গুনফল যদি ভেক্টর রাশি হয় তবে সেই গুণনকে ভেক্টর গুণন বা ক্রস গুণন বলে ।
\(\overrightarrow P\) ও \(\overrightarrow Q\) দুইটি ভেক্টর রাশি এবং এদের মধ্যবর্তী কোণ \(\alpha\) হলে,
ভেক্টর গুনফল, \(\overrightarrow P\times\overrightarrow Q=\left|\overrightarrow P\right|\times\left|\overrightarrow Q\right|\times\sin\alpha\times\widehat\eta\) \(\lbrack0\leq\alpha\leq\pi\rbrack\)
এখানে \(\eta\) ডান হাতের নিয়ম অনুসারে পাওয়া যাবে ।
এখানে, \(\overrightarrow P\times\overrightarrow Q=\left|\overrightarrow P\right|\times\left|\overrightarrow Q\right|\times\sin\alpha\times\widehat\eta\)
যেহেতু, \(\sin90^o=1\)
তাই ও ভেক্টরদ্বয় পরস্পর লম্ব হলে, \(\overrightarrow P\times\overrightarrow Q=\left|\overrightarrow P\right|\times\left|\overrightarrow Q\right|\times\widehat\eta\) হবে ।
একই কারণে,
\(\widehat i\times\widehat j=1.1.\widehat k=\widehat k\)
\(\widehat j\times\widehat k=\widehat i\)
\(\widehat k\times\widehat i=\widehat j\)
এবং,
\(\widehat j\times\widehat i=-\widehat k\)
\(\widehat k\times\widehat j=-\widehat i\)
\(\widehat i\times\widehat k=-\widehat j\)
যেহেতু, \(\sin0^o=0\)
তাই \(\overrightarrow P\) ও \(\overrightarrow Q\) ভেক্টরদ্বয় পরস্পর সমান্তরাল হলে, \(\overrightarrow P\times\overrightarrow Q=0\) হবে ।
একই কারণে,
\(\widehat i\times\widehat i=1.1.\sin0^o.\widehat\eta=0\)
\(\widehat j\times\widehat k=0\)
\(\widehat k\times\widehat i=0\)
ভেক্টর গুণনে \(\eta\) একক ভেক্টরের দিক ডান হাতি নিয়ম দ্বারা নির্ধারিত হয় । উপরোক্ত ফলাফল গুলোও ডানহাতি নিয়ম দ্বারা ব্যাখ্যা করা যায় ।
দুইটি ভেক্টর পরস্পর সমান্তরাল হলে তাদের ক্রস গুণফল শূন্য হয় । এখানে ভেক্টরদ্বয়
\(\overrightarrow A=A_x\widehat i+A_y\widehat j+A_z\widehat k\)
\(\overrightarrow B=B_x\widehat i+B_y\widehat j+B_z\widehat k\)
হলে, নির্ণায়ক হতে আমরা পাই-
\(\frac{A_x}{B_x}=\frac{A_y}{B_y}=\frac{A_z}{B_z}\) হবে ।
ত্রিমাত্রিক ভেক্টরের ভেক্টর গুণ
মনে করি,
\(\overrightarrow A=A_x\widehat i+A_y\widehat j+A_z\widehat k\)
\(\overrightarrow B=B_x\widehat i+B_y\widehat j+B_z\widehat k\)
\(\overrightarrow A\times\overrightarrow B=\begin{bmatrix}\widehat i&\widehat j&\widehat k\\A_x&A_y&A_z\\B_x&B_y&B_z\end{bmatrix}=\widehat i\left(A_yB_z-A_zB_y\right)-\widehat j\left(A_xB_z-A_zB_x\right)+\widehat k\left(A_xB_y-A_yB_x\right)\)
ভেক্টর গুণ বা ক্রস গুনের প্রয়োগ
ত্রিভুজের ক্ষেত্রফল নির্ণয়
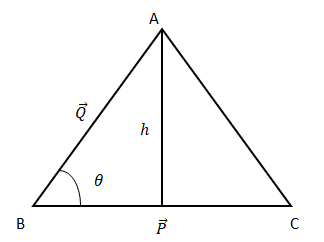
\(\overrightarrow P\) ও \(\overrightarrow Q\) ভেক্টরদ্বয় যদি কোন ত্রিভুজের দুইটি বাহু নির্দেশ করে
ত্রিভুজের ক্ষেত্রফল \(=\frac12\times\) ভূমি \(\times\) উচ্চতা \(=\frac12\times BC\times h=\frac12\times BC\times AB\times\sin\theta=\frac12\times P.Q.\sin\theta\)
ত্রিভুজের ক্ষেত্রফল \(=\frac12\times\left|\overrightarrow P\times\overrightarrow Q\right|\)
সামান্তরিকের ক্ষেত্রফল নির্ণয়
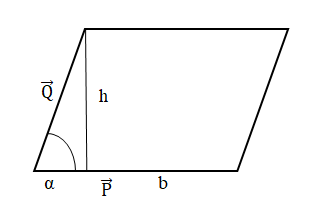
\(\overrightarrow P\) ও \(\overrightarrow Q\) ভেক্টরদ্বয় যদি কোন সামান্তরিকের সন্নিহিত বাহু নির্দেশ করে,
চিত্রে সামান্তরিকটিতে,
\(\sin\alpha=\frac h{\left|\overrightarrow Q\right|}\)
\(h=\left|\overrightarrow Q\right|\sin\alpha\) এবং \(b=\left|\overrightarrow P\right|\)
সামান্তরিকটির ক্ষেত্রফল \(=bh=\left|\overrightarrow P\right|.\left|\overrightarrow Q\right|.\sin\alpha=\left|\overrightarrow P\times\overrightarrow Q\right|\)
সামান্তরিকের ক্ষেত্রফল \(=\left|\overrightarrow P\times\overrightarrow Q\right|\)
অনুরূপভাবে, \(\overrightarrow{d_1}\) ও \(\overrightarrow{d_2}\) ভেক্টরদ্বয় যদি কোন সামান্তরিকের কর্ণ নির্দেশ করে তবে,
সামান্তরিকের ক্ষেত্রফল \(=\frac12\times\left|\overrightarrow{d_1}\times\overrightarrow{d_2}\right|\)
দুইটি ভেক্টরের লম্ব একক ভেক্টর নির্ণয়
ভেক্টর গুণে আমরা পেয়েছি-
\(\overrightarrow P\times\overrightarrow Q=\left|\overrightarrow P\right|\times\left|\overrightarrow Q\right|\times\sin\alpha\times\widehat\eta\)
এখানে \(\eta\) এর দিক, \(\overrightarrow P\) ও \(\overrightarrow Q\) উভয় ভেক্টরের সাথে লম্ব ।
\(\overrightarrow P\) ও \(\overrightarrow Q\) এর লম্ব একক ভেক্টর, \(\widehat\eta=\frac{\overrightarrow P\times\overrightarrow Q}{\left|\overrightarrow P\times\overrightarrow Q\right|}\)
স্কেলার এবং ভেক্টর গুনের সমন্নিত প্রয়োগ
ভেক্টর রাশির স্কেলার এবং ডট গুনের ধারনা থেকে বলা যায়,
তিনটি ভেক্টর \(\overrightarrow A\), \(\overrightarrow B\) এবং \(\overrightarrow C\) একই সমতলে অবস্থান করলে এদের যেকোনো দুইটির ভেক্টর গুন করে অপরটির সাথে স্কেলার গুন করলে ফলাফল শুন্য আসবে ।
অর্থাৎ, \(\overrightarrow A.\left(\overrightarrow B\times\overrightarrow C\right)=0\) হবে ।
বা, \(V=\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}=0\) হবে ।
এবং
\(\overrightarrow A\), \(\overrightarrow B\) এবং \(\overrightarrow C\) ভেক্টরত্রয় ঘনকের তিনটি ধার নির্দেশ করলে,
তবে ঘনকের আয়তন, \(V=\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}\)
১। m এর মান কত হলে \(\overrightarrow P=2\widehat i-3\widehat j+5\widehat k\) এবং \(\overrightarrow Q=2\widehat i+m\widehat j+\widehat k\) ভেক্টরদ্বয় পরস্পর লম্ব হবে ?
২। \(\overrightarrow P=\widehat i-2\widehat j+2\widehat k\) ভেক্টরটি অক্ষত্রয়ের সাথে যেসকল কোণ উৎপন্ন করে তা নির্ণয় কর ।
৩। \(\overrightarrow F=3\widehat i+10\widehat j-2\widehat k\) বল প্রয়োগে একটি কণা P(2,-1,3) বিন্দু থেকে Q(7,4,1) বিন্দুতে চলে গেল । এখানে কাজ নির্ণয় কর ।
৪। \(\overrightarrow P=2\widehat i+\widehat j-\widehat k\) এবং \(\overrightarrow Q=\widehat i-4\widehat k\) এর ভেক্টর গুণফলের মান নির্ণয় কর ।
৫। \(\overrightarrow P=3\widehat i+\widehat j-2\widehat k\) এবং \(\overrightarrow Q=6\widehat i+m\widehat j-4\widehat k\) ভেক্টরদ্বয় পরস্পর সমান্তরাল হলে m এর মান নির্ণয় কর ।
১। m এর মান কত হলে \(\overrightarrow P=2\widehat i-3\widehat j+5\widehat k\) এবং \(\overrightarrow Q=2\widehat i+m\widehat j+\widehat k\) ভেক্টরদ্বয় পরস্পর লম্ব হবে ?
সমাধান
যেহেতু, \(\overrightarrow P\) ও \(\overrightarrow P\) ভেক্টরদ্বয় পরস্পর লম্ব । তাই এদের ডট গুণফল শূন্য হবে ।
\(\overrightarrow P.\overrightarrow Q=0\)
বা, \(4-3m+5=0\)
\(m=3\)
২। \(\overrightarrow P=\widehat i-2\widehat j+2\widehat k\) ভেক্টরটি অক্ষত্রয়ের সাথে যেসকল কোণ উৎপন্ন করে তা নির্ণয় কর ।
সমাধান
\(\overrightarrow P\) ভেক্টরটি X-অক্ষের সাথে \(\theta_x\) কোণ উৎপন্ন করলে,
\(\widehat i.\overrightarrow P=\left|\widehat i\right|.\left|\overrightarrow P\right|.\cos\theta_x\)
বা, \(1=1.3.\cos\theta_x\)
\(\theta_x=\cos^{-1}\left(\frac13\right)\)
\(\overrightarrow P\) ভেক্টরটি Y-অক্ষের সাথে \(\theta_y\) কোণ উৎপন্ন করলে,
\(\widehat j.\overrightarrow P=\left|\widehat j\right|.\left|\overrightarrow P\right|.\cos\theta_y\)
বা, \(-2=1.3.\cos\theta_y\)
\(\theta_y=\cos^{-1}\left(-\frac23\right)\)
\(\overrightarrow P\) ভেক্টরটি Z-অক্ষের সাথে \(\theta_z\) কোণ উৎপন্ন করলে,
\(\widehat k.\overrightarrow P=\left|\widehat k\right|.\left|\overrightarrow P\right|.\cos\theta_z\)
বা, \(2=1.3.\cos\theta_z\)
\(\theta_z=\cos^{-1}\left(\frac23\right)\)
৩। \(\overrightarrow F=3\widehat i+10\widehat j-2\widehat k\) বল প্রয়োগে একটি কণা P(2,-1,3) বিন্দু থেকে Q(7,4,1) বিন্দুতে চলে গেল । এখানে কাজ নির্ণয় কর ।
সমাধান
সরণ, \(\overrightarrow s=\overrightarrow{PQ}=\overrightarrow Q-\overrightarrow P=\left(7-2\right)\widehat i+\left(4+1\right)\widehat i+\left(1-3\right)\widehat i=5\widehat i+5\widehat j-2\widehat k\)
কাজ, \(W=\overrightarrow F.\overrightarrow s=15+50+4=69\;J\)
৪। \(\overrightarrow P=2\widehat i+\widehat j-\widehat k\) এবং \(\overrightarrow Q=\widehat i-4\widehat k\) এর ভেক্টর গুণফলের মান নির্ণয় কর ।
সমাধান
\(\overrightarrow P\times\overrightarrow Q=\begin{vmatrix}\widehat i&\widehat j&\widehat k\\2&1&-1\\1&0&-4\end{vmatrix}=\widehat i(-4-0)-\widehat j(-8+1)+\widehat k(0-1)=-4\widehat i+7\widehat j-\widehat k\)
গুণফলের মান, \(\left|\overrightarrow P\times\overrightarrow Q\right|=\sqrt{\left(-4\right)^2+7^2+\left(-1\right)^2}=\sqrt{66}\)
৫। \(\overrightarrow P=3\widehat i+\widehat j-2\widehat k\) এবং \(\overrightarrow Q=6\widehat i+m\widehat j-4\widehat k\) ভেক্টরদ্বয় পরস্পর সমান্তরাল হলে m এর মান নির্ণয় কর ।
সমাধান
যেহেতু ভেক্টরদ্বয় পরস্পর সমান্তরাল,
তাই \(\overrightarrow P\times\overrightarrow Q=0\) হবে ।
বা, \(\overrightarrow P\times\overrightarrow Q=\begin{vmatrix}\widehat i&\widehat j&\widehat k\\3&1&-2\\6&m&-4\end{vmatrix}=0\)
বা, \(\widehat i(-4+2m)-\widehat j(-12+12)+\widehat k(3m-6)=0\)
বা, \(\widehat i(-4+2m)+\widehat k(3m-6)=0\)
এর মান শূন্য হতে হলে \(\widehat i\) এবং \(\widehat k\) এর সহগকে পৃথকভাবে শূন্য হতে হবে ।
সুতরাং,
\(-4+2m=0\)
\(m=2\)
অথবা,
\(3m-6=0\)
\(m=2\)
টপিকস - 2.12: অপারেটর, গ্রেডিয়েন্ট, ডাইভারজেন্স, কার্ল অপারেটর ।
অপারেটর
যে গাণিতিক চিহ্নের নিজস্ব কোন মান না থাকলেও কোন রাশির উপর ক্রিয়া করে তাকে অন্য রাশিতে পরিবর্তন করতে পারে অর্থাৎ কোন রাশির পরিবর্তন ব্যাখ্যা করতে পারে তাকে অপারেটর বলে । যেমনঃ \(\left(\sqrt\;\right),\;\left(\sin\right),\;\left(\;^3\right)\) ইত্যাদি ।
ভেক্টর ডিফারেন্সিয়াল অপারেটরঃ এই অপারেটরটি সার হ্যামিলটন প্রথম আবিস্কার করেন এবং গিবস নামকরণ করেন –“ডেল” । তবে এটি “ন্যাবলা” নামে ও পরিচিত । এর প্রকাশঃ-
ডেল বা ন্যাবলা, \(\overrightarrow\nabla=\frac{\partial\;}{\partial x}\widehat i+\frac{\partial\;}{\partial y}\widehat j+\frac{\partial\;}{\partial z}\widehat k\)
স্কেলার ক্ষেত্রঃ কোন ক্ষেত্রের সাথে সংশ্লিষ্ট ভৌত গুণ যদি স্কেলার হয়, তবে ঐ ক্ষেত্রকে স্কেলার ক্ষেত্র বলে ।
ভেক্টর ক্ষেত্রঃ কোন ক্ষেত্রের সাথে সংশ্লিষ্ট ভৌত গুণ যদি ভেক্টর হয়, তবে ঐ ক্ষেত্রকে ভেক্টর ক্ষেত্র বলে ।
ভেক্টরে তিনটি অপারেটরের প্রয়োগ রয়েছে । এগুলো হল- গ্রেডিয়েন্ট, ডাইভারজেন্স, কার্ল ।
গ্রেডিয়েন্ট, ডাইভারজেন্স এবং কার্ল অপারেটর
গ্রেডিয়েন্ট
যে ভেক্টর ক্ষেত্র অদিক রাশির সর্বাধিক বৃদ্ধির হার নির্দেশ করে তাকে গ্রেডিয়েন্ট বলে । [এটি স্কেলার ক্ষেত্রের উপর ক্রিয়া করে তাকে ভেক্টর ক্ষেত্রে পরিণত করে ।] এর প্রকাশ-
\(\varphi(x,y,z)\) যদি কোন ব্যবকলন যোগ্য স্কেলার ক্ষেত্র হয়, তবে এর গ্রেডিয়েন্ট,
\(grad\;\varphi=\;\overrightarrow\nabla\varphi=\left(\frac{\partial\;}{\partial x}\widehat i+\frac{\partial\;}{\partial y}\widehat j+\frac{\partial\;}{\partial z}\widehat k\right)\varphi=\frac{\partial\varphi\;}{\partial x}\widehat i+\frac{\partial\varphi\;}{\partial y}\widehat j+\frac{\partial\varphi\;}{\partial z}\widehat k\)
ডাইভারজেন্স
যে স্কেলার ক্ষেত্র দ্বারা ভেক্টর ক্ষেত্রের কোন বিন্দুতে ফ্লাক্সের প্রকৃতি জানা যায় তাকে ডাইভারজেন্স বলে । [এটি ভেক্টর ক্ষেত্রের উপর ক্রিয়া করে তাকে স্কেলার ক্ষেত্রে পরিণত করে ।] এর প্রকাশ-
\(\overrightarrow V=v_1\widehat i+v_2\widehat j+v_3\widehat k\) যদি কোন ভেক্টর ক্ষেত্র হয়, তবে –
\(div.\;\overrightarrow V=\;\overrightarrow{\nabla.}\overrightarrow V=\left(\frac{\partial\;}{\partial x}\widehat i+\frac{\partial\;}{\partial y}\widehat j+\frac{\partial\;}{\partial z}\widehat k\right).\left(v_1\widehat i+v_2\widehat j+v_3\widehat k\right)=\frac{\partial v_1\;}{\partial x}+\frac{\partial v_2\;}{\partial y}+\frac{\partial v_3\;}{\partial z}\)
ডাইভারজেন্স এর সাহায্যে একক আয়তনে কোন ভেক্টর রাশির কতটুকু ফ্লাক্স কোন দিকে অপসারিত হচ্ছে তা প্রকাশ করে । এটি দ্বারা একক সময়ে কোন তরল পদার্থের ঘনত্ব পরিবর্তনের হার বুঝায় । অর্থাৎ –
১। এর মান ধনাত্মক হলে, তরল পদার্থের আয়তন বৃদ্ধি পায় এবং ঘনত্ব হ্রাস পায় ।
২। এর মান ঋণাত্মক হলে, তরল পদার্থের আয়তন সংকুচিত হয় এবং ঘনত্ব বৃদ্ধি পায় ।
৩। এর মান শূন্য হলে, আগত ও নির্গত ফ্লাক্স সমান হয় । যাকে সলিনয়ডাল বলে ।
কার্ল
কার্ল একটি ভেক্টর রাশি যা কোন ভেক্টর ক্ষেত্রের ঘূর্ণনশীলতা নির্দেশ করে । অর্থাৎ কোন বিন্দুর চারিদিকে ভেক্টরটি কত বার ঘোরে কার্ল তা নির্দেশ করে । এর প্রকাশ-
\(\overrightarrow V=v_1\widehat i+v_2\widehat j+v_3\widehat k\) যদি কোন ভেক্টর ক্ষেত্র হয়, তবে –
\(Curl.\;\overrightarrow V=\;\overrightarrow\nabla\times\overrightarrow V=\left(\frac{\partial\;}{\partial x}\widehat i+\frac{\partial\;}{\partial y}\widehat j+\frac{\partial\;}{\partial z}\widehat k\right)\times\left(v_1\widehat i+v_2\widehat j+v_3\widehat k\right)=\begin{vmatrix}\widehat i&\widehat j&\widehat k\\\frac{\partial\;}{\partial x}&\frac{\partial\;}{\partial y}&\frac{\partial\;}{\partial z}\\v_1&v_2&v_3\end{vmatrix}=\widehat i\left(\frac{\partial v_3}{\partial y}-\frac{\partial v_2}{\partial z}\right)-\widehat j\left(\frac{\partial v_3}{\partial x}-\frac{\partial v_1}{\partial z}\right)+\widehat k\left(\frac{\partial v_2}{\partial x}-\frac{\partial v_1}{\partial y}\right)\)
কোন ভেক্টর ক্ষেত্রের কার্ল এর নতিমাত্রা শূন্য । অর্থাৎ, \(\overrightarrow\nabla.\left(\overrightarrow\nabla\times\overrightarrow V\right)=0\)
কোন ভেক্টরের কার্ল শূন্য হলে ভেক্টরটি অঘূর্ণনশীল হবে ।
১। \(P=2xyz+x^2y\) এর গ্রেডিয়েন্ট নির্ণয় কর । (1,2,0) বিন্দুতে গ্রেডিয়েন্টের মান কত ?
২। \(\overrightarrow P=3x\widehat i+my\widehat j+z\widehat k\) ভেক্টর ক্ষেত্রটির ডাইভারজেন্স নির্ণয় কর । m এর মান কত হলে ভেক্টরটি সলিনয়েড হবে ?
৩। \(\overrightarrow A=3x\widehat i+xy\widehat j+z^2\widehat k\) ভেক্টরটির কার্ল নির্ণয় কর ।
১। \(P=2xyz+x^2y\) এর গ্রেডিয়েন্ট নির্ণয় কর । (1,2,0) বিন্দুতে গ্রেডিয়েন্টের মান কত ?
সমাধান
P এর গ্রেডিয়েন্ট, \(grad\;P=\;\overrightarrow\nabla P=\left(\frac{\partial\;}{\partial x}\widehat i+\frac{\partial\;}{\partial y}\widehat j+\frac{\partial\;}{\partial z}\widehat k\right)P=\frac{\partial P\;}{\partial x}\widehat i+\frac{\partial P\;}{\partial y}\widehat j+\frac{\partial P\;}{\partial z}\widehat k\)
\(\overrightarrow\nabla P=(2yz+2xy)\widehat i+(2zx+x^2)\widehat j+2xy\widehat k\)
সুতরাং এর গ্রেডিয়েন্ট, \(\overrightarrow\nabla P=(2yz+2xy)\widehat i+(2zx+x^2)\widehat j+2xy\widehat k\)
(1,2,0) বিন্দুতে,
\(\overrightarrow\nabla P=(2.2.0+2.1.2)\widehat i+(2.0.1+1^2)\widehat j+2.1.2\widehat k=4\widehat i+\widehat j+4\widehat k\)
\(\left|\overrightarrow\nabla P\right|=\sqrt{4^2+1^2+4^2}=\sqrt{33}\)
(1,2,0) বিন্দুতে P এর গ্রেডিয়েন্টের মান \(=\sqrt{33}\)
২। \(\overrightarrow P=3x\widehat i+my\widehat j+z\widehat k\) ভেক্টর ক্ষেত্রটির ডাইভারজেন্স নির্ণয় কর । m এর মান কত হলে ভেক্টরটি সলিনয়েড হবে ?
সমাধান
\(\overrightarrow P\) এর ডাইভারজেন্স, \(=\overrightarrow\nabla.\overrightarrow P=\left(\frac{\partial\;}{\partial x}\widehat i+\frac{\partial\;}{\partial y}\widehat j+\frac{\partial\;}{\partial z}\widehat k\right).\left(3x\widehat i+my\widehat j+z\widehat k\right)=\frac{\partial(3x)}{\partial x}+\frac{\partial(my)}{\partial y}+\frac{\partial(z)}{\partial z}=3+m+1=m+4\)
সুতরাং \(\overrightarrow P\) এর ডাইভারজেন্স \(=m+4\)
\(\overrightarrow P\) ভেক্টরটি সলিনয়েড হলে এর ডাইভারজেন্স =0 হবে ।
\(\overrightarrow\nabla.\overrightarrow P=m+4=0\)
\(m=-4\)
৩। \(\overrightarrow A=3x\widehat i+xy\widehat j+z^2\widehat k\) ভেক্টরটির কার্ল নির্ণয় কর ।
সমাধান
\(\overrightarrow A\) এর কার্ল,
\(\overrightarrow\nabla\times\overrightarrow A=\begin{vmatrix}\widehat i&\widehat j&\widehat k\\\frac{\partial\;}{\partial x}&\frac{\partial\;}{\partial y}&\frac{\partial\;}{\partial z}\\3x&xy&z^2\end{vmatrix}=\widehat i\left[\frac{\partial\left(z^2\right)}{\partial y}-\frac{\partial\left(xy\right)}{\partial z}\right]-\widehat j\left[\frac{\partial\left(z^2\right)}{\partial x}-\frac{\partial\left(3x\right)}{\partial z}\right]+\widehat k\left[\frac{\partial\left(xy\right)}{\partial x}-\frac{\partial\left(3x\right)}{\partial y}\right]=\widehat i\times0-\widehat j\times0+\widehat k\times y=y\widehat k\)
১। দুইটি ভেক্টর রাশির প্রত্যেকের মান 5 একক । তারা একই বিন্দুতে পরস্পর \(120^o\) কোণে ক্রিয়া করছে । লব্ধির মান ও দিক নির্ণয় কর । [RUET:12-13] [MBSTU:12-13]
২। তিনটি সমান বল একটি বিন্দুতে ক্রিয়া করে ঐ বিন্দুকে সাম্যবস্থায় রেখেছে । বলত্রয়ের অন্তুর্ভূক্ত কোণ নির্ণয় কর । [RUET:11-12]
৩। দুইটি ভেক্টর রাশির বৃহত্তর ও ক্ষুদ্রতর লব্ধি যথাক্রমে 28 একক এবং 4 একক । রাশি দুইটি পরস্পর \(90^o\) কোণে কোন একটি বিন্দুতে ক্রিয়া করলে লব্ধির মান নির্ণয় কর । [CUET:15-16]
৪। দুইটি সমমানের ভেক্টর একটি বিন্দুতে ক্রিয়াশীল । এদের লব্ধির মান যে কোন একটি ভেক্টরের সমান । ভেক্টরদ্বয়ের মধ্যবর্তী কোণ নির্ণয় কর । [DU:11-12]
৫। দুইটি বলের লব্ধির মান 40 N । বলদ্বয়ের মধ্যে একটির মান 30 N । যদি এটি লব্ধির সাথে লম্ব বরাবর ক্রিয়া করে তবে অন্য বলটির মান নির্ণয় কর । [DU:10-11]
৬। দুইটি ভেক্টরের যোগফল ও বিয়োগফল একই হলে, এদের মধ্যবর্তী কোণ কত ? [PUST:15-16]
৭। 5 N ও 10 N দুইটি বল কোন কণার উপর ক্রিয়া করলে এদের লব্ধির ধারণা দাও । [DU:06-07]
৮। \(\overrightarrow P=\widehat i+2\widehat j-2\widehat k\) ও \(\overrightarrow P=3\widehat i+2\widehat j+2\sqrt3\widehat k\) ভেক্টর দুইটি পরস্পরের উপর লম্ব হলে, লব্ধি ভেক্টরের দিক নির্ণয় কর । [DU:07-08]
৯। ঘণ্টায় 1800 m বেগে 240 m প্রসস্থ একটি নদী প্রবাহিত হচ্ছে । ঘণ্টায় 3600 m বেগে সাঁতারে সক্ষম একজন সাঁতারু তার বিপরীত বিন্দুতে যেতে ইচ্ছুক । তিনি কোণ দিক বরাবর সাঁতার দিবেন এবং ঐ বিন্দুতে যেতে তার কত সময় লাগবে ? [BUET:03-04]
১০। একটি ইঞ্জিন চালিত নৌকার বেগ 14 km/h । একটি 7 km/h বেগের স্রোতযুক্ত নদী আড়াআড়ি ভাবে পার হতে নৌকাটিকে কোনদিকে চালনা করতে হবে এবং নদী পার হতে কত সময় লাগবে? [নদীর প্রস্থ 12.125 km] [CUET:04-05, 14-15]
১১। একটি নদীর স্রোতের বেগ 5 ms-1 । 10 ms-1 বেগের একটি নৌকাকে সোজাসুজি নদী পাড়ি দিতে 1 min 40 sec সময় লাগে । নদীর প্রস্থ কত ? [CUET:03-04]
