কাজ
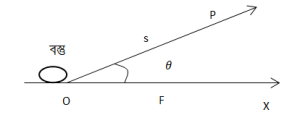
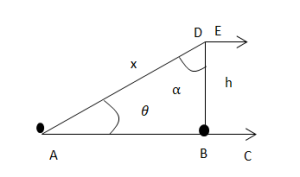
বল প্রয়োগের ফলে বস্তুর সরণ হলে বল এবং বলের দিকে বস্তুর সরণের উপাংশের গুণফলকে কাজ বলে।
আর্গ
কোনো বস্তুর উপর এক ডাইন বল প্রয়োগের ফলে যদি বলের দিকে বলের প্রয়োগ বিন্দুর এক সেন্টিমিটার সরণ হয় তাহলে সম্পন্ন কাজের পরিমাণকে এক আর্গ বলে।
কাজ-শক্তি উপপাদ্য
কাজ-শক্তি উপপাদ্যটি হলো-কোনো বস্তুর উপর ক্রিয়ারত লব্ধি বল কর্তৃক কৃত কাজ তার গতিশক্তির পরিবর্তনের সমান।
বলের দ্বারা কাজ
কোন বস্তুর উপর বল প্রয়োগের ফলে যদি প্রয়োগ বিন্দুর সরণ বলের অভিমুখে ঘটে তবে কৃতকাজকে বলের দ্বারা কাজ বলে।
শূন্য কাজ
বল প্রয়োগের ফলে যদি বস্তুর সরণ না হয় অথবা বলের প্রয়োগবিন্দু যদি সরণের উল্লম্ব অভিমুখে সরে যায় তবে শূন্য কাজ সম্পন্ন হয়।
একক কাজ
কোনো বস্তুর উপর একক বল প্রয়োগে বলের ক্রিয়া রেখা বরাবর যদি বস্তুটির একক সরণ ঘটে তবে যে পরিমাণ কাজ সম্পাদিত হয় তাকে একক কাজ বলে।
ঋণাত্মক কাজ
বল প্রয়োগের ফলে যদি বলের প্রয়োগ বিন্দু বলের ক্রিয়ার বিপরীত দিকে সরে যায় বা বলের দিকে সরণের ঋণাত্মক উপাংশ থাকে তবে যে কাজ সম্পাদিত হয় তাকে ঋণাত্মক কাজ বলে।
ধনাত্মক কাজ
কোনো বস্তুর উপর বল প্রয়োগের ফলে যদি বস্তুর সরণ হয় এবং বল ও সরণের মধ্যবর্তী কোণ যদি 90° অপেক্ষা কম হয় তবে বল দ্বারা সম্পন্ন কাজকে ধনাত্মক কাজ বা বলের দ্বারা কাজ বলে।
স্প্রিং বল
কোনো স্প্রিং-এর মুক্ত প্রান্তের সরণ ঘটালে স্প্রিংটি সরণের বিপরীত দিকে যে বল প্রয়োগ করে তাই স্প্রিং বল।
স্প্রিং ধ্রুবক
কোনো স্প্রিং-এর মুক্ত প্রান্তের একক সরণ ঘটালে স্প্রিংটি সরণের বিপরীত দিকে যে বল প্রয়োগ করে তাকে ঐ স্প্রিং- এর স্প্রিং ধ্রুবক বলে।
প্রত্যয়নী বল
কোনো স্প্রিংকে দৈর্ঘ্য বরাবর বিকৃত করলে স্থিতিস্থাপক ধর্মের দরুন প্রযুক্ত বলের বিপরীতে যে বলের উদ্ভব হয় তাকে প্রত্যায়নী বল বলে।
স্থিতিস্থাপক বিভব শক্তি
স্থিতিস্থাপক সীমার মধ্যে বস্তুর উপর বল প্রয়োগ করে বস্তুর বিকৃতি ঘটানোর জন্য যে পরিমাণ কাজ বস্তুর মধ্যে বিভব শক্তি হিসেবে সঞ্চিত থাকে তাকে স্থিতিস্থাপক বিভব শক্তি বলে।
গতিশক্তি
কোনো বস্তু গতিশীল অবস্থায় থাকার জন্য কাজ করার যে সামর্থ্য অর্জন করে তাকে গতিশক্তি বলে।
যান্ত্রিক শক্তি
কোনো বস্তুর অবস্থান ও গতির কারণে এর মধ্যে যে শক্তি থাকে তাই যান্ত্রিক শক্তি।
স্থিতিশক্তি
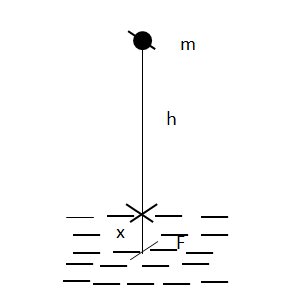
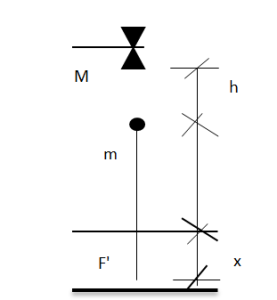
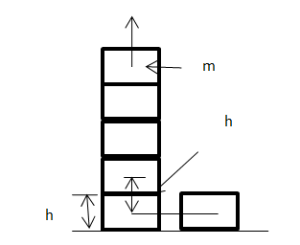
স্বাভাবিক অবস্থান বা আকৃতি হতে পরিবর্তন করে কোনো বস্তুকে অন্য কোনো অবস্থান বা আকৃতিতে আনলে ঐ বস্তুতে কিছু পরিমাণ শক্তি সঞ্চিত হয়। বস্তুর এ পরিবর্তিত অবস্থান বা আকৃতির জন্য বস্তুতে যে শক্তি সঞ্চিত থাকে তাকে ঐ বস্তুর স্থিতিশক্তি বলে।
ঋণাত্মক বিভব শক্তি
কোনো বস্তুকে ভূমি হতে নিচের দিকে নামানো হলে এটি যে বিভবশক্তি অর্জন করে তাকে ঋণাত্মক বিভবশক্তি বলে।
অভিকর্ষ কেন্দ্র
বল সবসময় একটি বিন্দুতে কাজ করে, এ বিন্দুকে বলের ক্রিয়া বিন্দু বলা হয়। পদার্থের ওজন বা অভিকর্ষ বলও একটি বল। তাই ওজনও একটি বিন্দুতে ক্রিয়া করে। এ নির্দিষ্ট বিন্দুকেই বস্তুর অভিকর্ষ কেন্দ্র বলে।
শক্তির অপচয়
শক্তির এক রূপ হতে অন্যরূপে রূপান্তরের সময় এর সামান্য কিছু অংশ এমনভাবে রূপান্তরিত হয় যা কোনো কাজে আসে না। শক্তির এ অকার্যকর রূপান্তরকে শক্তির অপচয় বলে।
ক্ষমতা
কোনো উৎস বা সিস্টেম একক সময়ে যে কাজ সম্পাদন করে তাকে তার ক্ষমতা বলে।
অশ্বক্ষমতা কাকে
প্রতি সেকেন্ডে 746 জুল কাজ করার ক্ষমতাকে এক অশ্বক্ষমতা বলে।
এক ওয়াট
কোনো সিস্টেম এক সেকেন্ড সময়ে এক জুল কাজ সম্পন্ন করলে ঐ সিস্টেমের ক্ষমতাকে এক ওয়াট বলে।
কিলোওয়াট-ঘন্টা
এক কিলোওয়াট ক্ষমতাসম্পন্ন কোনো যন্ত্র এক ঘণ্টা কাজ করলে যে শক্তি ব্যয় হয় তাকে এক কিলোওয়াট ঘণ্টা বলে।
সংরক্ষণশীল বল
যে বল কোনো বস্তুর উপর ক্রিয়া করলে তাকে যেকোনো পথে ঘুরিয়ে পুনরায় প্রাথমিক অবস্থানে আনলে বল কর্তৃক কাজ শূন্য হয় তাকে সংরক্ষণশীল বল।
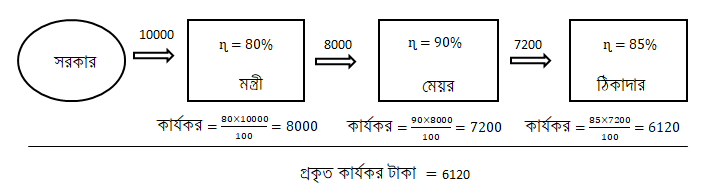
কর্মদক্ষতা
কোনো ব্যবস্থা বা যন্ত্র থেকে প্রাপ্ত মোট কার্যকর শক্তি এবং ব্যবস্থায় বা যন্ত্রে প্রদত্ত মোট শক্তির অনুপাতকে ঐ ব্যবস্থার বা যন্ত্রের কর্মদক্ষতা বলে।